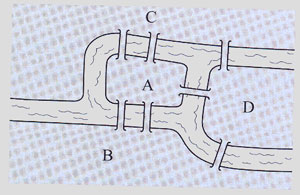
Tzv. problém královeckých mostů formuloval r. 1735 L.Euler jako důkaz sporem, tedy nepřímá metoda důkazu (reductio ad absurdum).
Město Královec bylo rozděleno řekou Pergel sedmi mosty na čtyři vzájemně propojené celky:
Je možné projít městem tak, aby trasa vedla přes každý ze sedmi mostů právě jednou ? Pokud přemýšlíte o nekonečném zkoušení různých tras,
zapomeňte na to. Euler dokázal, že se této práci lze vyhnout a to právě užitím důkazu sporem.
Představme si, že úloha nějaké řešení má. Tzn., že existuje trasa, která začíná v některé ze čtyř částí města A,B,C,D a končí v některé
jiné (může to být ta samá část), přičemž vede přes každý ze sedmi mostů právě jednou.
Je jasné, že nejméně dvě ze čtyř částí nebudou ani výchozí ani cílové. Do této z jedné částí naše trasa několikrát zavítá a opět ji opustí, což
znamená, že z/k tomuto městu musí vést sudý počet mostů. Jenomže tuto vlastnost nemá ani jedna ze čtyř částí Královce (5 a 3). Takže trasa s požadovanými
vlastnostmi neexistuje !
P.S.: tedy již existuje: dnešní Kaliningrad má po své rekonstrukci po 2. světové válce mostů jen pět ... :-)