1089: myslete si nějaké trojciferné číslo, kde se první od poslední číslice liší alespoň o dvě; napište jej v převráceném
tvaru a poté odečtěte menší od většího; výsledné číslo této operace napište opět v převráceném tvaru a obě čísla sečtěte: vždy vyjde výsledek 1089
příklad: číslo 236, převrácené 632; 632 - 236 = 396; převrácené 693; 693 + 396 = 1089
A proč to tak je ? Napišme si trojciferné číslo jako součin stovek, desítek a jednotek; tedy 100a + 10b + 1c (v našem případě s číslem 236: a = 2, b = 3, c = 6 a
pokud se číslo zapíše v převráceném tvaru získáme analogicky 100c + 10b + 1a; jelikož se v dalším kroku čísla od sebe odečítají, lze celou operaci zapsat jako
100a + 10b + c - 100c - 10b - a = 99(a - c) a protože a, c jsou celá čísla získáme vždy nějaký násobek čísla 99 a trojciferné násobky čísla 99 jsou:
198, 297, 396, 495, 594, 693, 792 a 891. Je zřejmé, že součtem prvního a posledního čísla je vždy 9, takže když provedeme poslední část triku a k výsledku
přičteme číslo převrácené, dostaneme vždy devět stovek z prvních číslic, devět jednotek z číslic posledních a dvakrát devadesát z prostředních číslic, tedy:
900 + 9 + 180 = 1089
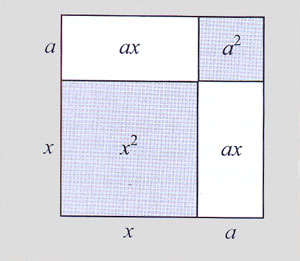
(a + x)2 je notoricky známá algebraická rovnice a každý si ji jistě pamatujeme ze školy. Možná by
někdo z vás byl schopen i doplnit rozklad ... (a + x)
2 = a
2 + 2ax + x
2
Pokud vás však zajímá proč je to zrovna takto a chcete rozklad pochopit, pomůže vám následující obrázek:
Každý ví, že obsah čtverce se počítá a.a, tedy a
2 a pokud si stranu a rozdělíme na dva libovolně velké díly, získáme právě
zápis (a + x) a dále je to již zcela jasné ...
důkaz; matematický důkaz - jeden z nejdůležitějších odkazů řecké geometrie; proč je tak nutné v matematice užívat důkazů ?
Je totiž velice snadné dospět k nesprávnému závěru ... Podívejme se na obrázek:
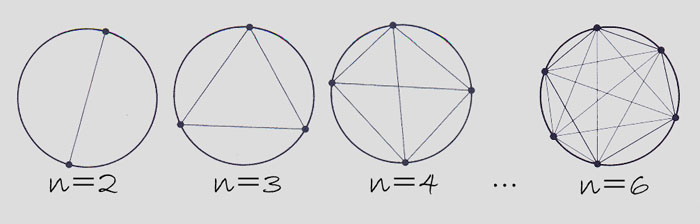
vezměme kruh a vyznačme na jeho obvodu dva body (označíme jako n), které spojíme úsečkou - v kruhu tak vzniknou dvě oblasti (označíme jako o)
nyní vyznačme body tři a opět spojíme každé dva z nich úsečkami - kruh je rozdělen na čtyři oblasti
pokračujeme se čtyřmi body (osm oblastí) a s pěti body (16 oblastí) ...
když tuto "posloupnost" zapíšeme jako n = 2 / o = 2; n = 3 / o = 4; n = 4 / o = 8; n = 5 / o = 16 vidíme zde jasnou závislost: pokud zvýšíme počet bodů
na kružnici o jeden, zvýší se počet oblastí dvojnásobně... avšak ejha ! když n = 6 pak o = 31 a ne třicetdva jak jsme logicky předpokládali
zde přichází na řadu důkaz, resp. obecný vzorec pro výpočet oblastí z výše uvedeného příkladu zní:
1/24(n
4 - 6n
3 + 23n
2 - 18n + 24)
elipsa - slovo známe všichni, jak elipsa vypadá, ví možná polovina z nás. Slovy ji lze popsat jako 'rozpláclou kružnici' a
pokud ani teď nevíte, tak se podívejte na obrázek
kuželosečky. Teď už víte jak elipsa vypadá, ale zkuste si ji
nakreslit bez pomocí umělohmotné šablony... Jak na to ? Řekové o elipse věděli úplně všechno a také znali metodu její konstrukce
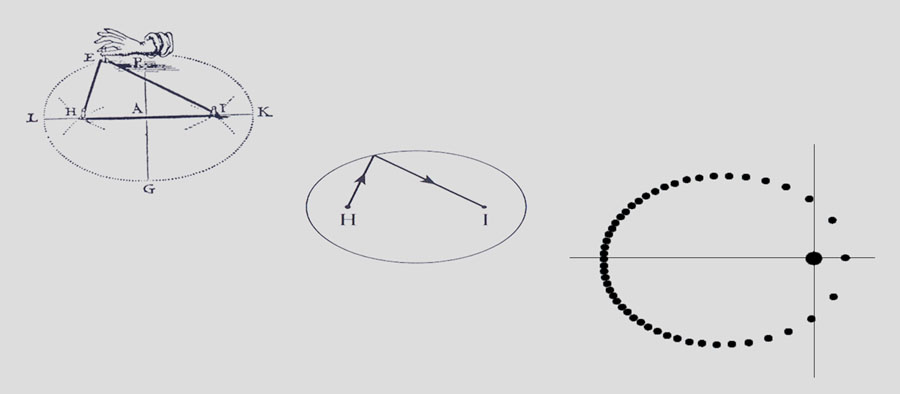
(Řekové považovali elipsu za vznešnou křivku) - na obrázku vlevo je Van Schootenova elipsa (Exercitationumm Mathematicorum, 1657)
Pokud sestrojíme eliptické zrcadlo a umístíme zdroj světla do bodu H, pak se všechny paprsky odrazí do bodu I a naopak (obrázek uprostřed).
J.Kepler (17. stol.) prokázal pečlivou analýzou, že planety se pohybují kolem Slunce po elispe, a navíc, Slunce se nachází přesně ve společném
ohnisku (obrázek napravo). Navíc zjistil, že každá planeta zrychluje svůj pohyb po oběžné dráze, když se blíží ke Slunci a zpomaluje, když se vzdaluje.
Kepler dále odvodil, že výseče (pomyslná čára spojující Slunce a planetu) vymezené pohybem této 'čáry' za stejnou jednotku času mají stejnou plochu.
Pokračování k tématu 'elipsa' je pod heslem 'gravitace'.
gravitace; pro pokračování ve čtení tohoto hesla je nutné (!) přečíst heslo 'elipsa' ...
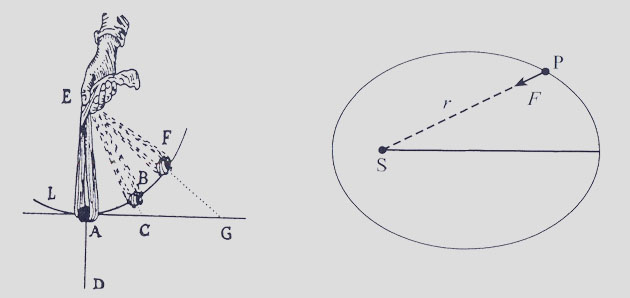
Proč by se měly planety pohybovat po křivkách (elipsách) ? Točíme-li kamenem zavěšeném v uzlíku, působí na něj síla ve směru ke středu otáčení E a
právě tato síla drží kámen na jeho dráze (nebylo-li by této síly, odletěl by po tečně ACG, obr. vlevo - Descartes; Principy filosofie, 1644):
Tato úvaha vedla k závěru, že dráhy planet má na svědomí "nějaká" síla ... Nyní obr. vpravo - začala se objevovat myšlenka, že by Slunce (S) mohlo působit nějakou
"gravitační" přitažlivou silou (F) na každou jednotlivou planetu. Jak by závisela síla F na vzdálenosti od Slunce (r) ? Kepler nakonec definoval, že F je přímo
úměrná veličině 1/r
2 (což později potvrdil I.Newton, 1729)
matematika vs. praxe - standardní úloha na výpočet maxim a minim v diferenciálním počtu zní: jak dopravit kmen stromu
(jehož tloušťku zanedbáváme) ve vodorovné poloze z jedné ulice šířky a do druhé ulice šířky b, které spolu svírají pravý úhel. Jak dlouhý může
být kmen, abychom s ním mohli ještě zahnout zan roh ? Po několika početních úkonech získáme konečnou rovnici
√(
3√a
2 +
3√b
2)
3
básník A.Strindberg převádí tuto úlohu do praxe: "je to půvabná hádanka, ale žádný chytrý dělník se nezastaví a nebude to vypočítávat - on to
prostě zkusí !"
diferenciální a integrální počet v praxi - jednoduchým pokusem si lze znázornit numerický vztah, který se projevuje
při pohybu (ačkoli úplný matematický popis jeho obecného pozadí vyžaduje dostatečnou znalost diferenciálního a inregrálního počtu)
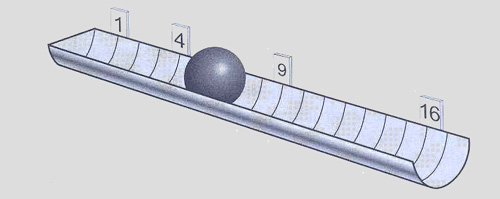
Vezměme delší žlab a nakloňme jej - pak položme na vrchol žlabu míček a pusťme jej. Označme místo, kam se míček dostal právě po jedné sekundě a
tuto vzdálenost použijedme jako jednotkové měřítko k označení po celé délce žlabu. Provedeme-li nyní celý pokus znovu, zjistíme, že za 1 s
se míček dostane ke značce 1, za 2 s se míček dostane ke značce 4 ... za 3 s ke značce 9, za 4 s ke značce 16 ... Obecný vztah je zde zcela jasný:
po n sekundách se míček při svém pohybu dostane na místo určené n
2 a tento vztah platí pro libovolný sklon žlabu.
Optické klamy - zde by bylo na místě zařadit heslo do "zábavná geometrie", ale ponechme jej zde.
Podívejte se na obrázek
úsečka a rozhodněte jaká úsečka je delší (AB nebo BC) ? Odpověď: obě jsou stejně dlouhé
Tentýž případ je vyznačen na obrázku
kruhy, opět je obsah vnitřních kružnic v obou případech shodný...
A nyní dva klasické příklady optických klamů - na obrázku
Fraserova spirála byste se asi museli přesvědčit
s pomocí kružítka, že se nejedná o spirálu, ale 'pouze' o jednotlivé kružnice; a na obrázku
kostky spočítejte, kolik
kostiček vidíte. Nyní si klikněte ještě jednou na tento
odkaz kde je tentýž obrázek s kostičkami, ale je otočen
o 180
o a opět je spočítejte; nakonec optická iluze
trojúhelníku - naše mysl
si doplnila úsečky a plochu, abychom vnímali obraz jako geometrický celek
Pí, π = 3,14159 ... to znají všichni, ale proč ... ?
vezměte libovolně dlouhý kus provazu a vyrobte z něj přesný kruh (techniku provedení nechám na vás, pokus se nepodaří přesný kruh, musíte počítat s odchylkou ve výsledku) a
změřte průměr tohoto kruhu (hodnotu označme A); následně změřte délku použitého provazu (hodnotu označme B); vydělte pak délku provazu průměrem kruhu a vyjde
vám číslo ... 3,14159...; matematicky vyjádřeno: B/A = π a protože se v geometrii počítá s poloměrem (zde tedy A/2) a poloměr se značí r a jelikož
hodnotu pí známe, chceme tedy spíš počítat obvod kruhu (zde B), můžeme rovnici zapsat ve tvaru "obvod kružnice" = 2πr a to už je známý
vzoreček ze základní školy. Kruh či kružnice - tam je pí jako "doma", ale možná vás překvapí, že se pí vyskytuje i v počtu pravděpodobnosti:
1. Vezměte linkovaný papír s roztečí (chcete-li výškou) mezi jednotlivými linkami s hodnotou 'x' a házejte na něj např. sirky délky rovněž 'x'; potom
pravděpodobnost toho, že sirka protne nějakou linku je 2/π
2. Nemáte-li po ruce sirky či linkovaný sešit, tak si zkuste házet korunou; hodíte-li si 2n krát, kde 'n' je (pokud možno) veliké číslo, pak pravděpodobnost,
že vám padne přeně n-krát panna a n-krát orel je přibližně rovna 1/√nπ
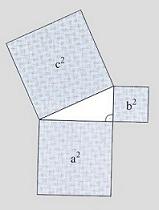
Pythagorova věta, definice: nechť a,b,c jsou strany pravoúhlého trojúhelníku, z nichž c je nejdelší; potom platí, že
a
2 + b
2 = c
2 neboli, že součet obsahu čtverců nad oběma
odvěsnami (a,b) se rovná obsahu čtverce nad přeponou (c); všem známý obrázek:
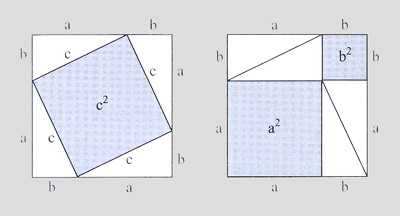
a nyní důkaz zábavný: vezměme čtverec a x b a do něj vložíme čtyři kopie trojúhelníku dle obrázku výše; zbyde pak čtverec o ploše c
2;
posuňme nyní tři trojúhelníky jako dlaždičky na podlaze do pozice jaká je na druhém obrázku a obsah plochy, která vznikla přesunutím trojúhelníků je nyní
čtverec o ploše a
2, resp. b
2 a jelikož se nezměnila velikost žádné strany trojúhelníků, musí
být tato plocha stejná jako před posouváním, tedy c
2; a
2 + b
2 =
c
2
rovnice, která neplatí ...
Láhev (označme L) s vínem (V) stojí 52 Kč. Přitom víno stojí o 50 Kč více než lahev. Kolik stojí víno bez láhve ? Odpověď 50 Kč není správná, tedy alespoň podle rovnice:
Jestliže jsme v první větě definovali: L + V = 52, a v druhé tedy V = L + 50, pak:
L + V = 52
L = 52 - V
V = L + 50 (dosadíme z první rovnice L)
V = (52 - V) + 50
V + V = 52 - 50
2 V = 2
V = 2/2 = 1
52 - 1 = 51; Víno bez láhve stojí 51 Kč ... :-)
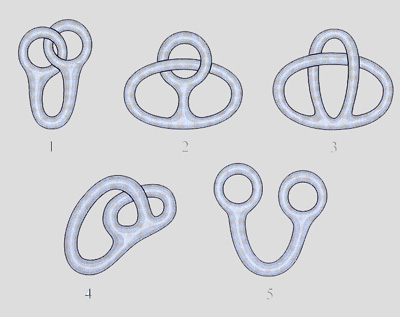
topologie je odvětví geometrie "na gumové podložce" (více samostatný odkaz v sekci 'matematické pojmy'); krásným
příkladem je známý hlavolam dvou propojených (elastických) oček, které lze spojitou deformací přeměnit na očka nepropojená; místo dalších slov
postačí obrázek
1 = 0 ?
nechť 'a' i 'b' je rovno 1, protože a = b, platí, že
b
2 = a + b
protože 'a' je rovno samo sobě, platí, že
a
2 = a
2
nyní odečtěme první rovnici od druhé
a
2 - b
2 = a
2 - ab
po úpravě obou stran rovnice, dostaneme
(a + b)(a - b) = a(a-b)
pro zkrácení vydělíme obě strany rovnice výrazem (a - b)
a + b = a tedy b = a - a, b = 0
jak je možné, že jsme definovali na počátku a, b = 1 a nyní zjistíme, že b = 0, resp. 1 = 0 ?
není zde žádný chyták ani matematická chyba ! Jediný problém nastal v okamžiku, kdy jsem celou rovnici dělili výrazem (a - b).
Protože jsme definovali a, b = 1, pak tedy 1 - 1 = 0 a jak je známo, nulou se dělit nesmí ...