



| A | ||||||||||||||||||||||||||
| abakus | řec. deska pokrytá prachem (pův. význam slova); typ historického počítadla, určené k jednoduchým matematickým operacím; byla používána již ve starém Řecku a Římě, Egyptě a Mezopotámii a do nedávné doby také v Číně, Japonsku a Rusku | |||||||||||||||||||||||||
| absolutní hodnota | a.h. reálného čísla znamená absolutní vzdálenost na ose (grafu) od bodu 0; a.h. čísla a se značí |a| a je definována jako |a| = a pro a ≥ 0, |a| = -a pro a ≤ 0; absolutní hodnota komplexního čísla x + iy je √(x2 + y2), což je vzdálenost bodu [x, y] od počátku v Gaussově rovině | |||||||||||||||||||||||||
| Achilles a želva | též paradox Achilles a želva; Zenon; jedna z prvních (5. stol. př.n.l.) historicky dochovaných úvah o 'nekonečnu' - (rychlý) Achilles nikdy nedohoní (pomalou) želvu, pokud ta má určitý náskok a definujeme, že pokud Achilles urazí jednotkovou vzdálenost, pak želva urazí vždy polovinu této vzdálenosti; vzniká tak řada nekonečně malých hodnot avšak nikdy se nepřiblíží k nule (1/2 - 1/4 - 1/8 ... 1/64 ...) | |||||||||||||||||||||||||
| algebra | vzniklo z arabského slova al-jabr = dát dohromady; matematický obor, v němž se zobecňují a rozšířují pojmy čísla a operace, známé z aritmetiky, pomocí vyjádření čísel písmeny a operací znaménky; tento termín vyjadřoval původně jeden z algoritmů úprav rovnic (9. stol., Al Chvárizmí; spis Al-jabr wa´lmuqabala) a do konce 19. stol. se algebrou rozuměla nauka o řešení rovnic | |||||||||||||||||||||||||
| algebraická topologie | H.Poincaré; ke studiu a klasifikaci variet využívá algebraické pojmy (fundamentální grupa variety) | |||||||||||||||||||||||||
| algoritmus | schéma nebo systematický postup k uskutečnění výpočtu; návod jak z rovnice získáme výsledek vyjádřený číselně, jak za
pomoci základních matematických ůkonů, různě na sebe navazujících, vyřešíme postupně i nejsložitější úlohu; a. musí splňovat požadavek,
že každý, kdo podle něho počítá, musí dojít ke správnému výsledku (za předpokladu, že neudělá početní chybu) slovo samotné pochází z jména arabského matematika Al-Chvárizmí |
|||||||||||||||||||||||||
| analysis situs | viz topologie (zde) | |||||||||||||||||||||||||
| antilogaritmus | a. čísla a je číslo, jehož logaritmem je a; např. 3 je dekadický logaritmus č. 1000 a tedy 1000 je antilogaritmus čísla 3 | |||||||||||||||||||||||||
| antinomie | rozpor mezi důsledky dvou zákonů, pravidel nebo tvrzení považovaných za pravdivé | |||||||||||||||||||||||||
| anuloid | též torus; plocha vytvořená rotací kružnice kolem přímky, která leží v její rovině a nemá s ní společný bod | |||||||||||||||||||||||||
| apokalyptické číslo | patří k tzv. sugestivním číslům užívaných především numerology 666 + 6 + 6 + 6 = (6 - 6/6)(6 + 6 + 6)/6 + 6(6 + 6 + 6)/6 + (6 + 6/6)(6 + 6 + 6)/6 |
|||||||||||||||||||||||||
| apotema | poloměr kružnice vepsané pravidelnému mnohoúhelníku; nebo: délka pobočné hrany jehlanu | |||||||||||||||||||||||||
| aproximace | přibližné určení veličiny nebo čísla dvěma hodnotami určujícími interval, v němž je obsažena; čím menší je tento interval, tím je aproximace přesnější | |||||||||||||||||||||||||
| ARCLP test | test prvočíselnosti - testuje se zda je dané číslo prvočíslem (počítačová metoda - pracuje se s čísly řádově na 1000 míst) (srovnej Lucasův-Lehmerův test) |
|||||||||||||||||||||||||
| Archimédův axióm | tvrdí, že jsou-li dány dvě délky a, b, pak existuje vždy celočíselný násobek menší z nich, který
je větší než délka druhá zevšeobecněno: přičtete-li číslo k sobě samému, převýší výsledek vždy jakékoli původní číslo (pozor, neplatí pro nulu !) |
|||||||||||||||||||||||||
| Aristotelova logika | ač jménem ukazuje k Aristotelovi, není jasné nakolik se na ní podílel Aristoteles sám a nakolik jeho následovníci; podle Aristotela
se důkaz (viz zde), racionální či logický postup, skládá z řady tvrzení, přičemž každé z nich logicky navazuje na předchozí a zároveň se
řídí určitými logickými pravidly nejedná se o zcela správnou definici logiky (viz zde) |
|||||||||||||||||||||||||
| aritmetika | nauka o číslech; zabývá se jejich definicí, způsoby jejich zápisu a operacemi s nimi prováděnými | |||||||||||||||||||||||||
| asteroida | viz křivka (zde) | |||||||||||||||||||||||||
| asymptota | tečna rovinné křivky v jejím nevlastním bodě (projektivní rovina) | |||||||||||||||||||||||||
| axióm | též postulát; tvrzení, které se nedokazuje, ale přijímá se jako pravdivé (např.: dvěma různými body prochází právě jedna přímka) | |||||||||||||||||||||||||
| axióm úplnosti | též Cauchyho axióm; Cauchy formálně vytvořil reálná čísla z čísel racionálních tím, že pomocí rafinovaného postupu přidal na racionální číselnou osu nové body, které byly limitami těch posloupností racionálních čísel, jejichž členy se k sobě neomezeně blíží | |||||||||||||||||||||||||
| axiomatická metoda | metoda, která se používá při tvoření teorie ze základních pojmů a z axiómů pomocí definic a vět; tato metoda je typická pro matematické teoretické konstrukce | |||||||||||||||||||||||||
| axonometrie | druh rovnoběžného promítání v deskriptivní geometrii; průmětna je různoběžná se všemi osami zvolené soustavy souřadnic a neprochází jejím počátkem; pro svou názornost se používá v technice a v architektuře | |||||||||||||||||||||||||
| B | [ nahoru ] | |||||||||||||||||||||||||
| Bézoutova věta | B.v. tvrdí: zbytek při dělení polynomu ƒ(x) polynomem x - a je roven ƒ(a); důsledky: polynom ƒ(x) je dělitelný polynomem x - a beze zbytku, právě když je číslo a kořenem polynomu ƒ(x); je-li p/q (v základním tvaru) racionální kořen polynomu ƒ(x) s celočíselnými koeficienty, pak p dělí absolutní člen a q dělí koeficient u nejvyšší mocniny polynomu ƒ(x) |
|||||||||||||||||||||||||
| bikvadratická rovnice | b.r. je rovnice ve tvaru ax4 + bx2 + c = 0, kde x je neznámá, a,b,c, jsou daná reálná čísla taková, že a ≠ 0; b.r. se řeší převedením na kvadratickou rovnici | |||||||||||||||||||||||||
| bilión | 1012 | |||||||||||||||||||||||||
| binom | dvojčlen, mnohočlen o dvou členech nebo součet dvou jednočlenů (monomů) | |||||||||||||||||||||||||
| binomická rovnice | viz ROVNICE | |||||||||||||||||||||||||
| binomická věta | též Newtnova věta; věta o rozvinutí výrazu (a + b)n, kde n je přirozené číslo | |||||||||||||||||||||||||
| bisekanta | přímka, která spojuje dva body prostorové křivky | |||||||||||||||||||||||||
| bod | základní geometrický pojem, který není definován; Euklides jej popsal jako "to, co nemá části"; v analytické geometrii je bod dán svými souřadnicemi; v obecnějších matematických oborech se často bodem rozumí prvek libovolného zkoumaného prostoru | |||||||||||||||||||||||||
| bod vratu | b.v. algebraické křivky je dvojnásobný bod křivky, v němž má křivka jedinou tečnu; je-li křivka trajektorií pohybu bodu, pak bod opisující křivku mění v bod vratu směr svého pohybu v opačný (křivka se "vrací") | |||||||||||||||||||||||||
| Booleova algebra | B.a. je množina I, na niž jsou dány dvě operace, které se označují + a x (tato znaménka nesouvisí nijak
se znaménky pro sčítání, resp. násobení) a splňují pro libovolné prvky a,b,c množiny I následující zákony:
|
|||||||||||||||||||||||||
| brachystochrona | viz cykloida (zde) | |||||||||||||||||||||||||
| Brianchonova věta | projektivní geometrie, Ch.J.Brianchon B.v. tvrdí: vedeme-li ke kuželosečce šest tečen a1, ..., a6, pak spojnice průsečíků a1a2 ad. procházejí jedním bodem "jestliže strany šestiúhelníku procházejí střídavě dvěma body, pak se přímky, které spojuji protilehlé vrcholy, protínají v jednom bodě" |
|||||||||||||||||||||||||
| C | [ nahoru ] | |||||||||||||||||||||||||
| Cavalieriův princip | uvažujme dvě tělesa T1, T2 a rovinu α; jestliže pro každou rovinu rovnoběžnou s α má její průnik s tělesem T1 stejný obsah jako její průnik s tělesem T2, pak obě tělesa mají stejný objem | |||||||||||||||||||||||||
| celočíselné okruhy | matematická logika; soustava objektů, která vyhovuje daným axiomům pro aritmetiku celých čísel | |||||||||||||||||||||||||
| CMI | Clay Mathematics Institute; více viz zde 'problémy tisíciletí' | |||||||||||||||||||||||||
| Cramerovo pravidlo | používá se k řešení soustav lineárních rovnic s pomocí determinantů | |||||||||||||||||||||||||
| cykloida | (transcedentní) rovinná křivka popsaná jako dráha bodu P pevně spojeného s kruhem C, který se kotálí po pevné přímce r | |||||||||||||||||||||||||
| číselná soustava | soustava slov, symbolů a konvencí, pomocí nichž se čtou a zapisují čísla; konvence jsou nezbytné, protože přirozených čísel je nekonečně mnoho a bylo by nemožné pro každé z nich mít název a symbol; existuje mnoho číselných soustav (desítková, šestnáctková, dvacítková, dvojková aj.) a u starověkých národů ukazuje úroveň jejich aritemtiky (Mayové - šedesátková, Babylóňané - dvacítková) | |||||||||||||||||||||||||
| číslice | též cifra; grafický znak pro zápis čísel; v desítkové soustavě se užívá tzv. arabských číslic, znaků, které představují čísla od jedné do devíti; později byla zaveden symbol pro nulu (L.Piánský) | |||||||||||||||||||||||||
| číslo | pojem, který se během historie matematiky stále vyvíjel a zobecňoval více viz: druhy čísel historie a vývoj čísel |
|||||||||||||||||||||||||
| čtvercová čísla | pro Pythagorejce se jednalo o základní numerologická čísla; tvoří se postupným sčítáním lichých čísel, tedy 4 (1+3), 9 (1+3+5) ... | |||||||||||||||||||||||||
| čtverec čísla | druhá mocnina | |||||||||||||||||||||||||
| čtyřroh | v projektivní geometrii útvar tvořený čtyřmi body, z nichž žádné tři neleží v jedné přímce, a všemi přímkami, které spojují dvojice těchto bodů; zmíněné čtyři body jsou vrcholy čtyřrohu a přímky jsou strany | |||||||||||||||||||||||||
| čtyřstěn | viz mnohostěn | |||||||||||||||||||||||||
| čtyřstran | v projektivní geometrii útvar duální k čtyřrohu; je tvořen čtyřmi přímkami, z nichž každé dvě se protínají v některém z vrcholů | |||||||||||||||||||||||||
| čtyřúhelník | mnohoúhelník o čtyřech stranách; pro konvexní č. existují čtyři zvláštní případy:
|
|||||||||||||||||||||||||
| čtverec | má všechny vlastnosti obdélníku i kosočtverce; jedná se o pravidelný čtyřúhelník | |||||||||||||||||||||||||
| D | [ nahoru ] | |||||||||||||||||||||||||
| Dedekindův řez | více viz ČÍSLA (reálná čísla) | |||||||||||||||||||||||||
| definice | vysvětlení určitého termínu, které se opírá o termíny už známé, dříve zavedené | |||||||||||||||||||||||||
| délka úsečky | vzdálenost jejich koncových bodů | |||||||||||||||||||||||||
| délka oblouku | limita (pokud existuje) délek lomených čar složených z n úseček a vepsaných danému oblouku, jestliže n →
∞ a délka každé úsečky lomené čáry se blíží nule; obecně d.o. křivky o rovnici y = ƒ(x) se určuje
na základě stejné myšlenky pomocí integrálního počtu; jsou-li a,b x-ové souřadnice koncových bodů oblouku,
a < b, pak délka oblouku je ∫ab √{1 + [ƒ´(x)]2}dx, kde ƒ´(x) je derivace funkce ƒ(x) |
|||||||||||||||||||||||||
| Délský problém | pozornost geometrů upoutával již ve starověku (3. stol. př.n.l.); problém spočívá v sestrojení hrany krychle, jejíž objem by byl dvojnásobkem objemu krychle, jejíž hranou je daná úsečka - tzv. reduplikace krychle; tento problém nelze řešit euklidovsky, tj. pouze pravítkem a kružítkem; název pochází od bájného požadavku zdvojení objemu krychlového oltáře na ostrově Délos a problém patří mezi tři klasické úlohy starověké matematiky (spolu s kvadraturou kruhu a trisekcí úhlu); konstrukci lze provést pomocí kisoidy (viz křivka); řešení: délka hledané úsečky je 3√2 | |||||||||||||||||||||||||
| derivace | funkce y = ƒ(x) vyjadřuje hodnotu proměnné y, které odpovídá dané hodnotě proměnné x patřící do definičního
oboru funkce ƒ v 17. stol. byl zaveden pojem d., aby byla vyjádřena okamžitá rychlost změny funkce; pojem d. byl přesně definován v 19. stol. (Cauchy, Bolzano) na základě jimi zpřesněného pojmu limity; je-li dána funkce ƒ(x) definována na nějakém intervalu a bod x0 je vnitřní bod tohoto intervalu, pak limita relativního přírůstku funkce ƒ limh → 0[ƒ(x0 + h) - ƒ(x0)]/h se nazývá derivace funkce ƒ v bodě x0, pokud tato limita existuje a je vlastní |
|||||||||||||||||||||||||
| deskriptivní geometrie | d.g. řeší prostorové úhly tak, že je promítáním převede na úlohy v rovině; využívá zejména poznatků projektivní geometrie a její důležité aplikace najdeme v technice a architektuře | |||||||||||||||||||||||||
| determinant | d. čtvercové matice n-tého řádu [a11 a12 ... a1n] je součet všech součinů n prvků této matice takových, že v žádném z uvedených součinů se nevyskytují dva prvky z téhož řádku ani z téhož sloupce; přitom každý součin se násobí členem rs, kde r je znaménko příslušného pořadí prvních indexů a s je znaménko příslušného pořadí druhých indexů; d. úzce souvisejí s řešením soustav lineárních rovnic a dále se používají v analytické geometrii |
|||||||||||||||||||||||||
| dělení | dělění je obrácený početní výkon k násobení (viz zde) d. v dané množině čísel A je operace, která upořádané dvojici (a,b) prvků z A přiřazuje prvek c ∈ A (pokud existuje a je jediný) takový, že a = b.c, resp. a : b = c; číslo c se nazývá podíl čísel a , b, číslo a se nazývá dělenec a číslo b dělitel dělení se zbytkem v množině celých čísel přiřazuje uspořádané dvojici celých čísel (a,b), kde b > 0 (nulou nelze dělit !), uspořádanou dvojici celých čísel (c,r) tak, že a = bc + r, 0 ≤ r < b číslo r je zbytek při dělení čísla a číslem b; je-li r = 0, je a dělitelné číslem b beze zbytku |
|||||||||||||||||||||||||
| dělitelnost | vlastnost přirozených čísel a,b spočívající v tom, že a je dělitelné číslem b; číslo 0 je dělitelné všemi přirozenými čísly pro rychlé určení dělitelnosti čísel, aniž bychom prováděli dělení, používáme tzv. znaky dělitenosti:
|
|||||||||||||||||||||||||
| diferenciál | diferenciální počet - stanovuje průběh křivky, k čemuž je nutné znát tečnu a úhel, který svírá s osou x d. funkce: podle Leibnizovi klasické definice to byl přírůstek funkce ƒ(x) při nekonečně malé změně proměnné x; značil se dƒ(x) a při tehdejším vyjadřování byla derivace funkce ƒ(x) v bodě x rovna podílu diferenciálů funkcí ƒ(x) a x, což se dosud často zapisuje ƒ´(x) = dƒ(x) / dx; v dnesšním pojetí je d. funkce ƒ(x) v bodě x0 lineární funkce D(x) proměnné x D(x) = (x - x0)ƒ´(x0), kde ƒ´(x0) je derivace funkce ƒ(x) v bodě x0; graf této funkce je tečna grafu funkce ƒ(x) v bodě x0 |
|||||||||||||||||||||||||
| diferenciální struktura | topologie; globální schéma pro derivování | |||||||||||||||||||||||||
| dimenze | rozměr; bod má d. 0, přímka má d. 1, rovina má d. 2 a prostor má d. 3 | |||||||||||||||||||||||||
| direkční střed | d.s. tří kružnic, které leží v téže rovině a jejichž středy neleží v jedné přímce, je bod, v němž se protínají chordály jednotlivých dvojic těchto kružnic | |||||||||||||||||||||||||
| disjunktní množiny | jsou to množiny, které mají prázdný průnik, tj. nemají společný prvek | |||||||||||||||||||||||||
| diskriminant | viz rovnice, funkce | |||||||||||||||||||||||||
| divergence | obecně pojem označuje odchýlení, odklon, vzájemné vzdalování; v matematice označuje 'nekonečnost' | |||||||||||||||||||||||||
| dokonalá čísla | poprvé si jich "povšimli" Pythagorejci; jedná se o čísla, která byla součtem všech svých dělitelů s výjimkou sebe samého; 6 (1+2+3), 28 (1+2+4+7+14); staří Řekové znali ještě dvě další - 498 a 8128; dodnes je jich známo 33 a nevíme zda jich není nekonečně mnoho jako prvočísel; všechna sudá dokonalá čísla lze zapsat ve tvaru 2N(2N-1 - 1), kde N je určité přirozené číslo; L.Euler ukázal, že všechna sudá dokonalá čísla mají tento tvar, je-li 2N - 1 prvočíslo; není známo zda existují nějaká lichá dokonalá čísla | |||||||||||||||||||||||||
| druhá derivace | jedná se fakticky o derivaci derivace; složitější typy diferenciálních rovnic, uplatňující se především ve fyzice | |||||||||||||||||||||||||
| dualita | princip duality zaručuje, že určité tvrzení zůstává pravdivé, jestliže se v něm jisté pojmy nahradí pojmy k nim duálními; princip duality má velký význam v projektivní geometrii, protože v případě, kdy jedna věta je duální k jiné, umožňuje, aby důkaz jedné z nich zdůvodnil i druhou | |||||||||||||||||||||||||
| důkaz | úvaha, která zdůvodňuje platnost matematické věty, tj. platnost nějakého tvrzení na základě určitého
předpokladu; hlavní typy důkazů:
|
|||||||||||||||||||||||||
| důsledek | věta, která vyplývá bezprostředně z jiné věty | |||||||||||||||||||||||||
| dvojjehlan | těleso tvořené dvěma jehlany se společnou podstavou umístěnými v opačných poloprostorech vyťatých rovinou této podstavy a takovými, že spojnice jejich hlavních vrcholů je k této rovině kolmá | |||||||||||||||||||||||||
| dvojpoměr | nechť jsou na orientované přímce dány body A,B,C,D; pak dvojpoměr těchto bodů je poměr [CA→/ CB→] / [DA→/ DB→], označuje se (ABCD) je-li (ABCD) = -1, říkáme, že body A, B, C, D tvoří harmonickou čtveřici (čtveřinu) |
|||||||||||||||||||||||||
| E | [ nahoru ] | |||||||||||||||||||||||||
| e | konstanta; e = 2,718281..., definovaná jako e = (1/0!) + (1/1!) + (1/2!) + (1/3!) + ... = limn → ∞[1 + (1/n)]n jedná se o číslo iracionální, dokonce transcedentní; používá se jako základ tzv. přirozených logaritmů; exponenciální funkce ex má derivaci (ex) = ex, to vysvětluje souvislost s poločasem rozpadu radioaktivních látek, řezězovkou a dalšími aplikacemi |
|||||||||||||||||||||||||
| ekvipotence | vlastnost dvou množin A a B spočívající v tom, že existuje vzájemně jednoznačné zobrazení jedné z nich na
druhou - takové množiny nazýváme ekvipotentní nebo, že mají stejnou mohutnost e. množin je ekvivalence a třídy této ekvivalence odpovídají kardinálním číslům; dvě konečné množiny jsou ekvipotentní, právě když mají stejný počet prvků |
|||||||||||||||||||||||||
| ekvivalence | viz zde kongruence | |||||||||||||||||||||||||
| elipsa | kuželosečka, množina všech bodů v rovině, jejichž součet vzdáleností od dvou různých daných bodů (ohnisek) je stálý (větší než vzdálenost ohnisek 2e); elipsu lze analyticky vyjádřit rovnicí x2/a2 + y2/b2 = 1, kde a je hlavní poloosa, b vedlejší poloosa. Je-li a = b, vyjadřuje tato rovnice kružnici | |||||||||||||||||||||||||
| elipsoid | rotační e. je plocha vytvořená rotací elipsy kole její hlavní osy (spojnice ohnisek) nebo kolem její vedlejší osy
(kolmice na hlavní osu vedené středem elipsy); v prvním případě jde o rotační e. protáhlý, ve druhém případě o
zploštělý; někdy se rotačním e. rozumí rovněž těleso omezené touto plochou a v takovém případě lze mluvit o objemu rotačního e.:
|
|||||||||||||||||||||||||
| epicykloida | trajektorie pohybu bodu P, který je pevně spojen s kružnicí c a leží v její rovině, jestliže se kružnice
kotálí bez klouzání po pevné kružnici ležící v téže rovině a má s ní vnější dotyk jestliže bod P leží na kružnici c, jde o e. prostou, leží-li uvnitř c, jde o e. zkrácenou a leží-li vně c, jde o e. prodlouženou; v ptolemaiovském modelu vesmíru se po e. pohybovaly planety |
|||||||||||||||||||||||||
| Eratosthenovo síto | viz prvočísla | |||||||||||||||||||||||||
| Eukleidovy postuláty | pět základních Eukleidových postulátů (geometrie):
|
|||||||||||||||||||||||||
| Eukleidovy věty | týkají se pravoúhlých trojúhelníků; první tvrdí: čtverec sestrojený nad odvěsnou má stejný obsah jako obdélník, jehož jedna strana je shodná s přeponou a druhá s pravoúhlým průmětem příslušné odvěsny na přeponu; druhá tvrdí: čtverec sestrojený nad výškou (vedenou k přeponě) má stejný obsah jako obdélník, jehož strany jsou shodné s pravoúhlými průměty obou odvěsen na přeponu | |||||||||||||||||||||||||
| Eukleidův algoritmus | metoda pro výpočet největšího společného dělitele dvou přirozených čísel a, b; je-li a > b a z ≠ 0,
je zbytek při dělení čísla a číslem b, je NSD(a,b) = NSD(b,z); příklad: čísla 24 a 14; 24:14 = 1(10), 14:10 = 1(4), 10:4 = 2(2), 4:2 = 2(0), tedy NSD(24,14) = 2 |
|||||||||||||||||||||||||
| Euklidovská geometrie | v prostoru je součet úhlů v trojúhelníku vždy 180o; daným bodem v prostoru můžeme vést jednu rovnoběžku k dané přímce | |||||||||||||||||||||||||
| Euklidovská konstrukce | konstrukce pravítkem a kružítkem, protože ne všechny konstrukční úlohy se dají řešit e.k. (např.: Délský
problém, trisekce úhlu, kvadratura kruhu aj.); e.k. se skládá z konečného počtu elementárních e.k.:
|
|||||||||||||||||||||||||
| Eulerova funkce | E.f. přiřazuje každému přirozenému číslu n počet φ(n) všech přirozených čísel menších než n a nesoudělných s n; např.: φ(21) = 12, neboť z čísel 1, 2, ..., 20 je s číslem 21 nesoudělných 12 čísel (1,2,4,5,8,10,11,13,16,17,19,20); Eulerova věta tvrdí, že jsou-li a, n dvě nesoudělná přirozená čísla, pak číslo aφ(n) - 1 je dělitelné číslem n; jedná se o zobecnění Fermatovy věty, neboť pro každé prvočíslo p je zřejmě φ(p) = p - 1 |
|||||||||||||||||||||||||
| Eulerova přímka | přímka na níž leží střed kružnice trojúhelníku opsané, jeho těžiště a průsečík výšek (ortocentrum) | |||||||||||||||||||||||||
| Eulerova věta | E.v. z teorie čísel; viz Eulerova funkce | |||||||||||||||||||||||||
| Eulerova věta | E.v. tvrdí, že u konvexního mnohostěnu součet počtu vrcholů v a počtu stěn s se rovná součtu čísla 2 s počtem jeho hran h: v + s = h + 2 tato věta umožňuje dokázat, že existuje právě pět pravidelných mnohostěnů, aniž by se zkoumaly metrické vlastnosti |
|||||||||||||||||||||||||
| Eulerovo číslo | e = 2,718281828... ; E.č. je základem přirozeného logaritmu ln(x); je definováno jako limita posloupnosti (1 + 1/n) n : e = limn → ∞[1 + (1 / n)n] | |||||||||||||||||||||||||
| Eulerův vzorec | překvapující rovnost platící pro každé reálné číslo 'x': eix = cos x + i sin x takové spojení mezi goniometrickými funkcemi, matematickou konstantou 'e' a druhou odmocninou z čísla -1 (i) není zcela jistě náhodné; další pozoruhodnost bude patrná při dosazení za proměnnou 'x' hodnotou π a užitím vztahů cos π = -1 a sin π = 0: eiπ = -1 což lze upravit eiπ + 1 = 0 čímž nakonec dostaneme jednoduchou rovnici obsahující pět nejznámějších matematických konstant: 0, 1, π, i, e také z této rovnice vyplývá, že výsledkem mocniny s iracionálním základem a iracionálním imaginárním exponentem je celé číslo a dále platí, že umocníme-li imaginární základ na imaginární exponent, můžeme dostat reálné číslo velký význam E.v. tkví také v tom, že napomohl postupnému zavádění komplexních čísel do dalších matematických oblastí |
|||||||||||||||||||||||||
| evoluta | křivka, která je množinou středů křivosti křivky c, pokud c není kružnicí (u kružnice všechny středy křivosti
splývají s jejím středem); lze ji také definovat jako obálku všech normál křivky c; je-li křivka c´ evolutou křivky c, pak se c nazývá evolventa křivky c´ |
|||||||||||||||||||||||||
| evolventa | viz evoluta | |||||||||||||||||||||||||
| excentricita | viz kuželosečka | |||||||||||||||||||||||||
| exhaustivní metoda | Eudoxos; (geometrická) metoda k výpočtu plochy a objemu nejrůznějších tvarů před objevem integrálního počtu; česky by se mohla jmenovat jako "metoda vyčerpání" | |||||||||||||||||||||||||
| exponenciála | viz funkce, křivka | |||||||||||||||||||||||||
| exponent | viz mocnina | |||||||||||||||||||||||||
| extrapolace | viz interpolace | |||||||||||||||||||||||||
| extrémy funkcí | obecně se tímto názvem označují největší nebo nejmenší hodnoty, kterých určité funkce nebo veličiny mohou
nabýt v dané situaci; v geometrii se problémem maxim a minim zabývali už staří Řekové významným nástrojem pro vyhledávání e.f. je diferenciální počet a to především pro hledání e.f. více proměnných |
|||||||||||||||||||||||||
| F | [ nahoru ] | |||||||||||||||||||||||||
| faktoriál | f. přirozeného čísla n je součin všech přirozených čísel od 1 do n; značí se symbolem n! např.: 5! = 1 x 2 x 3 x 4 x 5 = 120, tedy faktoriál čísla 5 = 120; v případě, kdy n = 0, klademe n! = 1 (viz permutace) |
|||||||||||||||||||||||||
| fan-čen | Čína; metoda řešení soustav n lineárních rovnic s n neznámými, která je obsažena v traktátě "Matematika v devíti knihách" ze 2. stol. př.n.l.; díky použití této metody bylo nutné zavést číslo "fu" - záporná hodnota, resp. opačné číslo | |||||||||||||||||||||||||
| Fermatova domněnka též velká Fermatova věta |
F.d. tvrdí, že neexistují čtyři přirozená čísla n > 2, x, y, z splňující rovnost xn + yn = zn Fermat napsal, že objevil jednoduchý důkaz tohoto tvrzení, ale nebylo nikdy nalezeno; na počátku 20. století byla vypsána odměna za vyřešení tohoto problému; její sláva ji přivedla také do beletrie pro nematematickou veřejnost; teprve r. 1995 podal důkaz Andrew Wiles |
|||||||||||||||||||||||||
| Fermatova metoda nekonečného sestupu | postup důkazu Fermatovy domněnky (velké F. věty); metoda blízká matematické indukci pro ověření různých vztahů mezi přirozenými čísly | |||||||||||||||||||||||||
| (malá) Fermatova věta | F.v. tvrdí, že je-li p prvočíslo, které nedělí číslo a ∈ N0, pak
ap - 1 - 1 je dělitelno číslem p aplikace F.v. se užívá např. při šifrování či karetních tricích; komplexní důkaz malé Fermatovy věty předložil r. 1736 L.Euler |
|||||||||||||||||||||||||
| Fibonacciho posloupnost | Fibonacci, resp. jeho posloupnost je spojována s poněkud jednoduchou
matematickou úlohou, kterou předložil r. 1202 ve své knize 'Liber Abaci' (Kniha o abaku): sedlák vlastní párek králíků, kterým
stačí na dosažení dospělosti dva měsíce a od té doby jsou schopni produkovat každý měsíc novou dvojici králíků ... když tito
dospějí, plodí zase další atd.; otázka zní: kolik párů králíků se bude rodit v jednotlivých měsících ? První měsíc je jeden pár
králíků a dokud nedospějí (tj. druhý měsíc), nemohou se rozmnožit, během druhého měsíce je tedy stále jen jeden pár králíků;
začátkem třetího měsíce se králíci rozmnoží a již jsou tedy dva páry ... (první měsíc 1 pár, druhý měsíc stále 1 pár a třetí měsíc
již 2 páry; tedy 1 - 1 - 2 ...) F.p. je utvořena tímto způsobem: první dva členy jsou 0 a 1; další členy dostaneme tak, že každý z nich je součtem dvou předcházejících; máme tedy řadu: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ... členy této posloupnosti se vyskytují v mnoha konkrétních situacích Existuje zde však ještě jeden význam této posloupnosti - jakékoliv číslo dělené svým předchůdcem (platí pro vyšší hodnoty) dává hodnotu blížící se zlatému řezu, jehož hodnota je 1,61803... (např. 89/55 = 1,61818181 ...) |
|||||||||||||||||||||||||
| Fieldsova medaile | ocenění pro matematiky, které vyplňuje mezeru vzniklou absencí Nobelovy ceny za matematiku více viz laureáti Fieldsovy medaile (angl.) |
|||||||||||||||||||||||||
| fĺuent | viz fluxe | |||||||||||||||||||||||||
| fĺuxe | Newtonův styl diferenciálního počtu byl založen na tzv. fluxích (diferenciálech) matematických výrazů, které nazýval fluenty příklad fluxe je rovnice y = x2 + x + 1, kde jsou fluenty 'y' a 'x' a Newton předpokládal, že 'y' a 'x' se mění s časem |
|||||||||||||||||||||||||
| formalismus | formalistický přístup k matematice: omezení se na odvozování konečných závěrů ze systému prvotních axiomů | |||||||||||||||||||||||||
| Fourierova analýza | matematická teorie zabývající se nekonečnými řadami funkcí | |||||||||||||||||||||||||
| Fourierova věta | matematický princip popisující způsob rozkladu (zvukové) vlny na součet jednotlivých sinusových vln | |||||||||||||||||||||||||
| funkce | zobrazení do množiny reálných nebo komplexních čísel; více viz odkaz: FUNKCE |
|||||||||||||||||||||||||
| funkce dzéta | L.Euler, 1740; funkce určená pro výzkum struktury prvočísel; Eulerova funkce ζ přiřazuje každému reálnému číslu 's' většímu
než 1 jiné reálné číslo ζ(s); abychom spočítali ζ(s) pro dané 's', musíme spočítat hosnotu nekonečné řady: ζ(s) = 1/1s + 1/2s + 1/3s + ... Euler dokázal, že pro libovolné reálné číslo 's' se ζ(s) rovná nekonečnému součinu: 1 / (1 - 1/2s) x 1 / (1 - 1/3s) x 1 / (1 - 1/5s) x 1 / (1 - 1/7s) x ... přičemž tento součin obsahuje všechny činitele tvaru 1 / (1 - ps) |
|||||||||||||||||||||||||
| G | [ nahoru ] | |||||||||||||||||||||||||
| Galileiho miska | těleso, které se získá tím, že z rotačního válce, jehož výška je rovna poloměru podstavy, se oddělí polokoule téhož poloměru; objem G.m. je roven objemu rotačního kužele, jehož poloměr podstavy i výška jsou rovny poloměru zmíněné polokoule | |||||||||||||||||||||||||
| Gaussova - Lobačevského - Bolyaiova geometrie | v prostoru je součet úhlů v trojúhelníku menší než 180o;
neeuklidovský prostor; daným bodem v prosotoru můžeme vést více rovnoběžek k dané přímce 20. léta 19. stol.: N.I.Lobačevskij a J. Bolayi nezávisle na sobě definovali specifické druhy neeuklidovské geometrie 1854: B.Riemann uvedl neeuklidovskou geometrii na "pevnou půdu"; jeho přístup umožnil rozvinout geometrii do více než tří dimenzí |
|||||||||||||||||||||||||
| genus prostoru | pojem z topologie; topologický znak, který udává podobnost předmětů podle definicí (držadlo, díry) a ne podle odlišnosti zakřivení | |||||||||||||||||||||||||
| geodetická křivka | g.k. plochy je křivka, která leží na ploše a má tu vlastnost, že nejkratší cesta po ploše mezi dvěma blízkými body této křivky vede po oblouku této křivky | |||||||||||||||||||||||||
| geometrická řada | příklad nekonečné řady (viz zde), kde se každý následující člen liší od předcházejícího o určitý konstantní kvocient q: S = a + aq + aq2 + aq3 + ... |
|||||||||||||||||||||||||
| geometrické místo | starší název pro geometrický útvar, který je tvořen právě všemi body, které mají určitou vlastnost | |||||||||||||||||||||||||
| geometrická zobrazení | g.z. v rovině jsou vzájemně jednoznačná zobrazení roviny na sebe; F.Klein r 1872 (tzv. Erlangenský program)
klasifikoval g.z podle toho, které vlastnosti při nich zůstávají nezměněny - tzv. invarianty zobrazení rúzné druhy zobrazení, viz odkaz: GEOMETRICKÁ ZOBRAZENÍ |
|||||||||||||||||||||||||
| geometrie | lat. zeměměřictví; matematický obor, který se zabývá množinami bodů v rovině a v prostoru (geometrické útvary)
|
|||||||||||||||||||||||||
| GIMPS | Great Internet Mersenne Prime Search - Velké internetové hledání Mersennových prvočísel; celosvětový projekt k
hledání nejvyšších Mersennových prvočísel více stránky GIMPS |
|||||||||||||||||||||||||
| Goldbachova hypotéza | tvrdí, že každé sudé číslo větší než 2 lze vyjádřit jako součet dvou prvočísel více zde |
|||||||||||||||||||||||||
| goniometrické rovnice | viz trigonometrie (viz zde) | |||||||||||||||||||||||||
| Gödelova věta o neúplnosti | K.Gödel, 1931; dvě důležité matematické věty, které mají zcela výsadní postavení v celé moderní matematické logice;
důležitou roli však hrají v celé matematice, zejména pak v teorii modelů, aritmetice a v teorii množin tvrdí, že v každém dostatečně širokém axiomatickém systému lze najít nerozhodnutelné tvrzení, tj. takové, že pomocí vnitřních pojmů tohoto systému nelze dokázat ani toto tvrzení, ani jako negaci |
|||||||||||||||||||||||||
| grad (též gon) | jednotka velikosti úhlu, která se používá velmi zřídka (především v geodézii); je roven jedné setině velikosti pravého úhlu | |||||||||||||||||||||||||
| graf | g. je tvořen prvky nějaké množiny, tzv. uzly (též vrcholy), a některými dvojicemi uzlů, tzv. hranami; uzly se většinou znázorňují jako body v rovině a hrany jejich spojnicemi | |||||||||||||||||||||||||
| graf funkce | y = ƒ(x) je množina všech bodů v rovině, jejichž souřadnice jsou [x, ƒ(x)] | |||||||||||||||||||||||||
| grafické řešení | g.ř. rovnice umožňuje pomocí grafického znázornění určit přibližné řešení rovnice; užívá se ho především u nealgebraických rovnic | |||||||||||||||||||||||||
| Grassmanovy proměnné | pomocí G.p. je popisována supersymetrie prostoru, známé jako Grassmanovy dimenze běžná čísla komutují, tzn. že a x b = b x a, ale G.p. antikomutují, tedy a x b = -a x b |
|||||||||||||||||||||||||
| grupa | matematické objekty, které právě v deseti rozměrech mají pozoruhodné vlastnosti nejvyšší symetrie a jedinečnosti -
v jiných počtech rozměrů nejsou jejich souměrnosti tak dokonalé; více viz 'struktura' (zde) V 19. stol. (Evariste Galois) vyšlo najevo, že soubor všech symetrií daného objektu, tedy soubor všech transformací, při nichž se vzhled objektu nemění, má jisté zajímavé strukturální vlastnosti, které na konkrétním objektu nezávisí - tyto nové aritmetické struktury byly nazvány 'grupami' a později bylo vybudováno nové odvětví matematiky - teorie grup, které se jejich studiem zabývá Množina všech symetrií daného objektu tvoří jeho grupu symetrií - teorii grup lze aplikovat nejen na fyzické objekty, ale též to mohou být abstraktní matematické pojmy, rovnice nebo silová pole g. je soubor změn vyznačující se třemi vlastnostmi:
|
|||||||||||||||||||||||||
| Guldinovy věty | viz Pappovy věty (zde) | |||||||||||||||||||||||||
| H | [ nahoru ] | |||||||||||||||||||||||||
| harmonická čtveřice | viz dvojpoměr (zde) | |||||||||||||||||||||||||
| harmonická řada | nekonečná posloupnost čísel: 1/2, 1/3, 1/4, 1/5 ... ve 14. stol. se tuto řadu pokusil sečíst N.Oresme a zjistil, že ač se členy této posloupnosti blíží nule, výsledek součtu naopak směřuje k nekonečnu |
|||||||||||||||||||||||||
| Heronův vzorec | viz trojúhelník (zde) | |||||||||||||||||||||||||
| Hilbertovy axiómy | H.a. tvoří axiomatický základ pro vybudování geometrie; základními pojmy jsou bod přímka a rovina; H.a. jsou rozděleny do pěti skupin: a. incidence, a. uspořádání, a. shodnosti, a. spojitosti a postulát o rovnoběžkách | |||||||||||||||||||||||||
| Hilbertovy problémy | 8.8. 1900 v Paříži u příležitosti druhého světového kongresu matematiků pronesl německý matematik David Hilbert přednášku, do níž zařadil seznam 23 problémů, které považoval za nejdůležitější dosud nevyřešené otázky matematiky. Některé byly vyřešeny velmi brzy a některé z nich byly formulovány příliš nepřesně, takže na ně neexistuje jednoznačná odpověď. V r. 2000 již byly vyřešeny všechny H.p. až na jeden (problém prvočísel) - další pokračování pod heslem problémy tisíciletí | |||||||||||||||||||||||||
| Hilbertův prostor | D.Hilbert; "jakási" nekonečně-rozměrná obdoba Eukleidova trojrozměrného prostoru; pojem z matematické logiky, resp. formalismu úplný prostor se skalárním součinem |
|||||||||||||||||||||||||
| Hippokratovy měsíčky | útvary omezené dvěma oblouky kružnic nad stranami pravoúhlého trojúhelníku | |||||||||||||||||||||||||
| histogram | h. je způsob grafického znázornění | |||||||||||||||||||||||||
| hodinová aritmetika | viz zde modulární aritmetika | |||||||||||||||||||||||||
| Holdernossovo číslo | nejvyšší obecně vypočítané číslo; 1070 000 000 000 000; počet možných spojení mezi mozkovými neurony | |||||||||||||||||||||||||
| Hornerovo schéma | efektivní způsob výpočtu hodnoty mnohočlenu v daném bodě; je založeno na tom, že mnohočlen ƒ(x) = a0xn + a1xn-1 + ... an píšeme ve tvaru ƒ(x) = (...((a0x + a1)x + a2)x + ... + an -1)x + an počítáme-li postupně "zevnitř" čísla c0 = a0, c1 = c0x + a1, ..................... cn = cn-1x + an, bude poslední z nich, cn, hodnotou polynomu ƒ(x) v bodě x; podobným způsobem se dají počítat i hodnoty derivací polynomu a také dělit polynom lineárním polynomem |
|||||||||||||||||||||||||
| l´Hospitalovo pravidlo | G. l´Hospital; diferenciální počet; toto pravidlo odstranilo nedostatek problémových výrazů 0/0 - např.
výraz x/(sin x) v bodě x=0, pak i sin x = 0, tedy 0/0; při použití H.p. platí, že se tento zlomek přibližuje hodnotě 1/(cos x) proto, že
derivací x je 1 a cos x je zase derivací funkce sin x; pro x = 0 platí, že cos x = 1, takže celý výraz přechází na tvar 1/1 aplikací H.p. lze tedy řešit speciální výrazy jako ∞/∞, 00, 0∞, ∞0 |
|||||||||||||||||||||||||
| hra | matematický model konfliktní situace, v níž se každá strana snaží ovlinit průběh a výsledek určitého procesu ve svůj prospěch; teorie her odvozuje optimální strategie a praktické aplikace má především v ekonomii | |||||||||||||||||||||||||
| hranol | viz mnohostěn | |||||||||||||||||||||||||
| hranolec | viz prizmatoid | |||||||||||||||||||||||||
| hustě uspořádaná množina | h.u.m. je množina A uspořádaná tak, že k libovolným dvěma prvkům a,b množiny A takovým, že a je v daném uspořádání před b, existuje alespoň jeden prvek množiny A, který je za a a současně před b | |||||||||||||||||||||||||
| hvězdicovka | viz křivka | |||||||||||||||||||||||||
| hyperbola | kuželosečka; h. protíná osu x v bodech zvaných vrcholy hyperboly: A[-a, 0], B[a, 0]; a, b se nazývají
délka hlavní poloosy a délka vedlejší poloosy; číselná excentricita má hodnotu e/a a je větší než 1 obecná rovnice hyperboly: x2/a2 - y2/b2 = 1 nebo ve zvláštním případě: xy = k |
|||||||||||||||||||||||||
| hyperboloid (rotační) | r.h. je plocha vytvořená rotací hyperboly kolem její osy | |||||||||||||||||||||||||
| hypocykloida | h. je trajektorie pohybu bodu P, který je pevně spojen s kružnicí c a leží v její rovině, jestliže se kružnice c kotálí bez klouzání po pevné kružnici ležící v téže rovině a má s ní vnitřní dotyk (kružnice c leží uvnitř ní); jesltiže bod P leží na kružnici c, jde o h. prostou, leží-li uvnitř c, jde o h. zkrácenou, leží-li vně c, jde o h. prodlouženou | |||||||||||||||||||||||||
| hypotéza kontinua | G.Cantor, 1882; označována 'CH' (angl. Continuum Hypothesis); tvrzení se týká otázky, zda existuje nějaká množina, jejíž mohutnost je ostře mezi mohutností množiny přirozených čísel a mohutností množiny čísel reálných (neboli kontinua), a odpovídá na ni záporně | |||||||||||||||||||||||||
| hypotéza velkých čísel | P.Dirac (1937); "libovolná velká bezrozměrná čísla, která se vyskytují v
přírodě, jsou navzájem propojena jednoduchými matematickými vztahy, jejichž
převodní koeficient je blízký jedničce"; k vyslovení této hypotézy jej vedl
rostoucí počet tzv. kosmologických koincidencí; také ho motivovala tři velká bezrozměrná čísla a převzal je od A.Eddingtona:
|
|||||||||||||||||||||||||
| CH | [ nahoru ] | |||||||||||||||||||||||||
| charakteristika | celé části logaritmů (uváděné v tabulkách); podívej mantisa | |||||||||||||||||||||||||
| chordála | ch. dvou kružnic, množina bodů v rovině majících stejnou mocnost k oběma kružnicím; jestliže se dané dvě kružnice protínají ve dvou bodech A, B, chordála je pak přímka AB, dotýkající se kružnice v bodě T, pak ch. je jejich společná tečna v bodě T; ch. je vždy přímka kolmá ke spojnici středů kružnic; jsou-li kružnice soustředné, ch. je prázdná množina | |||||||||||||||||||||||||
| chyba | rozdíl mezi skutečnou hodnotou a (která může, ale nemusí být známa) a hodnotou a´ branou jako aproximace hodnoty a; např. bere-li se pro π = 3,14159... hodnota 3,14, je chyba menší než jedna setina, bere-li se 3,141, je chyba menší než jedna tisícina atd.; s ch. se setkáváme především v numerické matematice při zaokrouhlování a při nahrazování přesných hodnot přibližnými výsledky numerického procesu | |||||||||||||||||||||||||
| I | [ nahoru ] | |||||||||||||||||||||||||
| projektivní geometrie; každá přímka v rovině má svůj jediný bod v nekonečnu (viz též ideální přímka) | ||||||||||||||||||||||||||
| ideální přímka | projektivní geometrie; dvě libovolné rovnoběžné přímky se protínají ve svém společném bodě v nekonečnu a všechny tyto body v nekonečnu leží leží na jediné přímce v nekonečnu, tzv. i.p. (viz též ideální bod) | |||||||||||||||||||||||||
| imaginární číslo | pojem zavedl Descartes, jako pohrdavé označení pro druhé odmocniny záporného čísla (pojem beze smyslu) řešení kvadratických rovnic ve tvaru x2 + 1 = 0, kde dostáváme výsledek ±√-1 a symbolem pro druhou odmocninu z -1 se stalo písmeno 'i' - imaginární část také viz ČÍSLA |
|||||||||||||||||||||||||
| implikace | viz logika (zde) | |||||||||||||||||||||||||
| index | číslo, písmeno nebo jiný symbol užívaný k rozlišení matematických objektů; např. u členů posloupnosti a1, a2, a3 značí indexy 1, 2, 3 pořadí příslušného členu | |||||||||||||||||||||||||
| indukce | viz důkaz (zde) | |||||||||||||||||||||||||
| infinitezimální počet | nekonečně malý i. počet - zastaralý název pro diferenciální a integrlní počet | |||||||||||||||||||||||||
| inflexní bod | i.b. křivky nebo funkce je bod, v němž křivka přechází z jedné strany své tečny na druhou | |||||||||||||||||||||||||
| inkluze | vztah mezi množinami A, B, kdy jedna je podmnožinou druh, např. A ⊂ B | |||||||||||||||||||||||||
| integrál | integrální počet - slouží k výpočtu ploch omezených křivkami a objemů těles ohraničených křivou plochou
|
|||||||||||||||||||||||||
| interpolace | jedná se o postup, jímž se přibližně určuje hodnota funkce ƒ(x) v bodě x ∈ <a, b>, jsou-li
známy její hodnoty v jiných bodech intervalu <a, b> postup, kterým se hledá přibližně průběh funkce v intervalu <h, x1> pro h o málo menší než x1 nebo v intervalu (x2, k> pro k o málo větší než x2, známe-li průběh funkce v intervalu <x1, x2> se nazývá extrapolace |
|||||||||||||||||||||||||
| interval | jsou-li dána dvě čísla a < b , pak interval je množina všech čísel mezi a a b; interval se nazývá uzavřený, jestliže a a b do něj patří, a otevřený, jestliže do něho nepatří; interval může být analogicky s předchozím také polouzavřený | |||||||||||||||||||||||||
| invariance | označení pro situaci, v níž jsou jisté objekty neměnné při určitých událostech (viz zde invariant) neproměnnost jisté struktury či vlastnosti při změně; dále se ukazuje, že i. vede k zachování jisté veličiny v čase; během 19. stol. matematikové strávili hodně času klasifikováním všech možných typů změn a v konkrétní i v abstraktní podobě přezkoumali i. s nimi spojené - z této klasifikace vzniklo odvětví matematiky zvané dnes 'teorie grup' (viz zde grupa) každý z nejzákladnějších fyzikálních zákonů zachování je založen na nějaké invarianci, tzn. že existuje soubor změn tvořící grupu symetrie, který ponechává zákony pohybu nezměněny a vede k příslušnému zákonu zachování |
|||||||||||||||||||||||||
| invariant | pojem nebo vlastnost jistých pojmů neměnící se daným zobrazením; např., při posunutí je obrazem přímky opět přímka, tedy přímka je invariantem posunutí | |||||||||||||||||||||||||
| inverze | i. v pořadí, dvojice prvků, které jsou v tomto pořadí uspořádány obráceně než v základním pořadí; je-li i počet inverzí pak (-1)i je znaménko pořadí | |||||||||||||||||||||||||
| iracionální číslo | řec. ratio = poměr + předpona 'i' označuje zápor či opak, tedy 'nepoměrné'; příkladem i.č. je odmocnina ze dvou, tedy číslo,
které nelze zapsat jako podíl (zlomek) dvou přirozených čísel více viz čísla jako první objevil existenci i.č. řecký matematik Hippasus, který na tento "problém" narazil při řešení výpočtu úhlopříčky čtverce s jednotkovu délkou strany (12 + 12 = √2) |
|||||||||||||||||||||||||
| ireducibilni | nerozložitelný; např. i. polynom je polynom, který nelze vyjádřit jako součin dvou nebo více jiných polynomů s reálnými koeficienty | |||||||||||||||||||||||||
| iterace | opakované provádění operace nebo algoritmu | |||||||||||||||||||||||||
| izometrie | viz shodnost (zde) | |||||||||||||||||||||||||
| izomorfismus | budiž dána množina A, na níž je definována operace *; tzn., že libovolné uspořádané dvojici (m,n) prvků z A tato operace přiřazuje prvek m*n, rovněž z množiny A; dále budiž dána množina B taková, že existuje vzájemně jednoznačné zobrazení A na B, které prvkům m a n přiřazuje po řadě prvky m´ a n´, a operace ◊ na B, která uspořádané dvojici (m´, n´) přiřazuje prvek m´◊n´ z množiny B; jestliže prvek m´◊n´ odpovídá v tomto zobrazení prvku m*n říkáme, že toto zobrazení je izomofrismus struktury (A, *) na strukturu (B, ◊) a že tyto dvě struktury jsou izomorfní; v případě kdy A = B, takovýto i. nazýváme automofrismus | |||||||||||||||||||||||||
| izoperimetrický problém | která uzavřená křivka o dané délce ohraničuje oblast o maximálním obsahu ? Už ve starém Řecku Pappos vyslovil doměnku, že je to kružnice, což bylo potvrzeno až v 19. století pomocí diferenciálního a integrálního počtu | |||||||||||||||||||||||||
| J | [ nahoru ] | |||||||||||||||||||||||||
| jednočlen | viz monom (zde) | |||||||||||||||||||||||||
| jehlan | viz mnohostěn (zde) | |||||||||||||||||||||||||
| K | [ nahoru ] | |||||||||||||||||||||||||
| kalkul(us) | I.Newton, G.Leibniz; dělení nulou a sčítání nekonečného počtu nul; lat. slovo 'kalkulus' označuje 'oblázek', protože rané početní systémy bývaly prováděny pomocí fyzické manipulace s oblázky; k. tvoří základ dnešního diferenciálního počtu | |||||||||||||||||||||||||
| kardinalita | vlastní hodnota čísla, jeho výše; matematická mohutnost (srovnej: ordinalita) též viz odkaz ČÍSLA, přirozená čísla |
|||||||||||||||||||||||||
| kardinální číslo | viz odkaz ČÍSLA | |||||||||||||||||||||||||
| kardioida | viz křivka (zde) | |||||||||||||||||||||||||
| kartézské souřadnice | Descartes; matematický koncept popisu umístění bodu v rovině prostřednictvím dvojice čísel, které se obvykle udávají v závorkách (první číslo označuje polohu na vodorovné ose X a druhé číslo na kolmé ose Y) | |||||||||||||||||||||||||
| kartézský součin | k.s. dvou množin A a B je množina všech uspořádaných dvojic, jejichž první člen je prvek z A a druhý člen je prvek z B; zapisuje se A × B; může být rovněž B = A; v tom případě máme k.s. A × A | |||||||||||||||||||||||||
| kisoida | viz křivka (zde) | |||||||||||||||||||||||||
| klenec | viz romboedr (zde) | |||||||||||||||||||||||||
| klín | dvě poloroviny se společnou hraniční přímkou dělí prostor na dvě části, které se nazývají klíny | |||||||||||||||||||||||||
| klotoida (též Cornuova spirála) |
rovinná křivka, která má tu vlastnost, že součin jejího poloměru křivosti v bodě P a délky oblouku spojujícího bod P s počátkem O soustavy souřadnic je konstantní; má spirálovitý tvar a existují dva body A a B, k nimž se neomezeně přibližuje, aniž by je obsahovala | |||||||||||||||||||||||||
| Kochova křivka | fraktální geometrie, též 'Kochova vločka'; více viz křivky | |||||||||||||||||||||||||
| kolineace | vzájemně jednoznačné zobrazení mezi dvěma projektivními rovinami α a β takové, že bodům roviny α ležícím v přímce jsou přiřazeny body roviny β ležící opět v přímce; k. se zavádí též v prostoru | |||||||||||||||||||||||||
| kolmost | kolmé přímky jsou dvě různoběžné přímky, které dělí příslušnou rovinu na čtyři shodné úhly, které se pak nazývají pravé | |||||||||||||||||||||||||
| kombinace | k-prvková kombinace (kombinace k-té třídy) z n prvků je k-prvková podmnožina z n-prvkové množiny; počet všech
k-prvkových kombinací z n prvků je tzv. kombinační číslo (nk) = n! / k!(n-k)! kde vykřičník znamená faktoriál; k výpočtu kombinačního čísla se užívá tzv. "Pascalův trojúhelník" - toto schéma je již v čínských uebnicích z r. 1303; kombinace s opakováním - k-prvková k. s o. z n prvků je skupina k prvků dané n-prvkové množiny, kde se prvky mohou opakovat; počet všech k-prvkových k. s o. je roven (n + k - 1k) |
|||||||||||||||||||||||||
| komolý kužel | k.k. (jehlan) je část kužele (jehlanu) ležící mezi dvěmsa rovinami rovnoběžnými s rovinou jeho podstavy, které s ním mají více než jeden bod společný | |||||||||||||||||||||||||
| komplanární | k. se nazývají body, přímky nebo geometrické útvary ležící v téže rovině | |||||||||||||||||||||||||
| komplementární množiny | dvě množiny A a B, které jsou podmnožinami množiny C a jsou takové, že A ∩ B = ∅ a A ∪ B = C; množina A se nazývá doplňkem (tedy komplementem) množiny B vzhledem k C, množina B se nazývá doplňkem množiny A vzhledem k C | |||||||||||||||||||||||||
| komplexní čísla | viz čísla | |||||||||||||||||||||||||
| komplexní rovina | C.F.Gauss; konstrukce kartézské roviny (pravoúhlá soustava souřadnic), kde vodorovná osa představuje reálnou část komplexního čísla a svislá osa část imaginární; tedy komplexní číslo (1 - 2i) lze v této soustavě zobrazit | |||||||||||||||||||||||||
| komplexní varieta | matematický (topolgický) prostor; speciální případ dvourozměrné sféry (povrch třírozměrné koule) | |||||||||||||||||||||||||
| konečná aritmetika | viz zde modulární aritmetika | |||||||||||||||||||||||||
| kongruence | též ekvivalence; algebraický pojem zavedený K.F.Gaussem; značí se symbolem ≡ aby se nepletly operace sčítání a násobení v běžné aritmetice se stejnýmim operacemi v konečné aritmetice (viz zde), byl nahrazen znak rovnosti = symbolem relace kongruence ≡ |
|||||||||||||||||||||||||
| konchoida | viz křivka (zde) | |||||||||||||||||||||||||
| konstanta | lat. constans – stálý, neměnný; stálá, neproměnná veličina, buď absolutně (např. pí = 3,14159… – poměr obvodu kružnice ku jejímu průměru), nebo ve vztahu k proměnným daného mat. vzorce [např. u funkce f(x) = kx + q jsou konstantami q, k | |||||||||||||||||||||||||
| konvexní | k. je takový geometrický útvar, že úsečka spojující libovolné jeho dva body A a B náleží celá příslušnému útvaru; k. útvary jsou např. kruh, úsečka, vnitřek čtverce, koule ad.; průnik dvou k. útvarů je opět k. útvar | |||||||||||||||||||||||||
| kosekans | viz trigonometrie (zde) | |||||||||||||||||||||||||
| kosinus | viz trigonometrie (zde) | |||||||||||||||||||||||||
| kotangens | viz trigonometrie (zde) | |||||||||||||||||||||||||
| koule | k. je těleso vytvořené rotací kruhu kolem jeho průměru; střed a poloměr tohoto kruhu jsou střed a poloměr koule; povrch koule se nazývá kulová plocha - množina bodů, jejichž vzdálenost od středu koule je rovna jejímu poloměru; tětiva koule je libovolná úsečka, jejíž krajní body leží na kulové ploše - tětiva procházející středem k. se nazývá průměr k. | |||||||||||||||||||||||||
| kružnice | geometrické místo bodů v rovině, které mají stejnou vzdálenost (poloměr k.) od bodu O této roviny (střed k.) více viz odkaz: KRUŽNICE budeme-li uvažovat kružnici na souřadnicových osách x,y, pak kružnice se středem v počátku a poloměrem r má rovnici x2 + y2 = r2 |
|||||||||||||||||||||||||
| křivka | pojem, jehož vymezení prošlo v historii matematiky složitým vývojem - hlavní příčinou byla snaha vyloučit
některé paradoxní případy; několik pojetí pojmu křivka:
k. lze klasifikovat podle jejich rovnice jako algebraické, transcedentní a algebraické; k. lze také definovat pomocí jejich tečen a v tomto případě se nazývá obálka prostorová křivka je k., která neleží v jedné rovině jednoduchá křivka může být vyjádřena jako trajektorie bodu P, kterou bod P může proběhnout, aniž by prošel dvakrát týmž bodem (k. otevřená) nebo tak, že se vrátí do výchozího bodu po proběhnutí této křivky tak, že mezitím žádným jiným bodem neprojde více než jednou (k. uzavřená) Jordanova k. je jednoduchá uzavřená k.; Jordanova věta tvrdí, že pro každou jednoduchou uzavřenou křivku a libovolná křivka, která spojuje bod uvnitř a s bodem vně a, protíná křivku a více viz odkaz: ROVINNÉ KŘIVKY |
|||||||||||||||||||||||||
| kužel (rotační k.) | těleso vytvořené rotací pravoúhlého trojúhelníku kolem jedné jeho odvěsny; tato odvěsna se nazývá výška k.; druhá odvěsna je poloměr podstavy a přepona je povrchová úsečka kužele | |||||||||||||||||||||||||
| kuželosečka | vzniká (jak již jejich název napovídá) různými řezy provedeným v kuželu, příp. dvojkuželu: kruh, elipsa, parabola či hyperbola
(též viz obrázek) průnik kruhové kuželové plochy s o vrcholu O s rovinou α; podle vzájemné polohy α a s rozlišujeme různé typy kuželoseček:
|
|||||||||||||||||||||||||
| kvadrant | k. v kartézské soustavě souřadnic je každý z vnitřních pravých úhlů sevřených souřadnicovými osami; obvykle se číslují (vždy počet 4) | |||||||||||||||||||||||||
| kvadratura | k. je transformace rovinného útvaru ve čtverec, který má stejný obsah jako tento útvar; termín k. lze užívat všude, kde se počítá obsah, což se často dělá pomocí určitých integrálů - proto se někdy k. rozumí numerický výpočet určitého integrálu | |||||||||||||||||||||||||
| kvadratura kruhu | sestrojení čtverce, který má stejný obsah jako daný kruh; v historii matematiky bylo mnoho pokusů o euklidovské řešení (pomocí pravítka a kružítka) tohoto problému, ale r. 1882 byla dokázána transcedentnost čísla pí a tím i nemožnost euklidovského řešení k.k.; problém lze řešit např. s pomocí křivky, tzv. Hippiovy kvadratrigy | |||||||||||||||||||||||||
| kvadrika | algebraická plocha, jejíž rovnice v kartézské soustavě souřadnic je druhého stupně; reálná k., která není degenerovaná (tj. není tvořena dvojicí rovin), patří k některému z pěti typů: elipsoid, eliptický paraboloid, hyperbolický paraboloid, jednodílný hyperboloid a dvoudílný hyperboloid | |||||||||||||||||||||||||
| kvaterniony | matematické objekty, které zavedl Hamilton r. 1853 jako rozšíření pojmu komplexního čísla; jsou dány
čtveřicemi reálných čísel a, b, c, d z nichž je vytvořen výraz q = a + bi + cj + dk, kde i, j, k jsou symboly, které lze násobit podle pravidel daných tabulkou
k. mají aplikace v mechanice a uplatňují se v teorii grup |
|||||||||||||||||||||||||
| L | [ nahoru ] | |||||||||||||||||||||||||
| lemma | pomocná věta, o nichž se opírá důkaz silnější či obecnější věty | |||||||||||||||||||||||||
| Lieova algebra | Lieova algebra je matematická struktura - vektorový prostor V spolu se bilineárním zobrazením [] : V x V → V | |||||||||||||||||||||||||
| leminskáta | viz křivka (zde) | |||||||||||||||||||||||||
| limita | pojem vyjadřující, že se hodnoty blíží libovolně blízko k nějakému bodu; vložením symbolu 'lim' před řadu čísel
oddělujeme cestu od jejího cíle; poprvé s myšlenkou limity přišel d´Alemebert l. funkce je základním pojmem matematické analýzy; zhruba řečeno, limita funkce ƒ(x) v bodě c je číslo, k němuž se blíží hodnoty ƒ(x) při x → c l. posloupnosti čísel {an} je číslo, ke kterému se blíží členy posloupnosti při n → ∞ |
|||||||||||||||||||||||||
| lineární | termín užívaný ve vztahu k mnohočlenům, rovnicím a soustavám rovnic; mnohočlen se nazývá lineární vzhledem k proměnné x, jestliže se tato proměnná vyskytuje v každém jeho členu nejvýše v první mocnině | |||||||||||||||||||||||||
| logaritmus | je-li dáno číslo a > 0, a ≠ 1, je jednoznačně definováno reálné číslo y takové, že ay
= x, kde x je dané kladné číslo; takové číslo y se nazývá logaritmus čísla x o základu a; zápis:
y = logax dekadický (Briggsův) logaritmus má základ 10 a značíme jej log x přirozený (Napierův) logaritmus má základ e a značíme jej ln x (někdy též lg x) základní vlstnosti při počítání s logaritmy:
|
|||||||||||||||||||||||||
| logika (matematická) | matematický obor, který, chápán jako formalizace logických operací, má svůj původ v myšlenkách Leibnize; l. zkoumá
především výroky, které se mezi sebou spojují pomocí logických spojek a vytvářejí tak nové výroky:
|
|||||||||||||||||||||||||
| lomená čára | jsou-li dány navzájem různé body A1, A2, ..., An, pak sjednocením úseček A1 A2, ..., An-1 An je otevřená l.č.; přidáme-li k ní ještě úsečku A1 An, dostáváme uzavřenou lomenou čáru; ta určuje mnohoúhelník | |||||||||||||||||||||||||
| loxodroma | na rotační válcové ploše je to křivka, která protíná každou tvořící přímku pod týmž úhlem - válcová šroubovice; na kulové ploše je to křivka, která protíná všechny polokružnice spojující dva protilehlé body plochy pod týmž úhlem; l. na kulové ploše má význam pro navigaci | |||||||||||||||||||||||||
| Lucasův-Lehmerův test | test prvočíselnosti - testuje se zda je dané číslo prvočíslem; tuto metodu lze použít jen na Mersennova čísla a počítá se v řádech miliónu míst (srovnej ARCLP test) | |||||||||||||||||||||||||
| Ludolfovo číslo (π) | je definováno jako poměr mezi délkou a průměrem kružnice; π je iracionální a transcedentní;
k výpočtu se používá nekonečného součinu π/2 = (2/1)(2/3)(4/3)(4/5)(6/5)(6/7) ... a dále součtu nekonečné řady či řetězového zlomku |
|||||||||||||||||||||||||
| M | [ nahoru ] | |||||||||||||||||||||||||
| magický čtverec | jedná se o číselný čtverec s následujícími vlastnostmi: v každém políčku je přirozené číslo, každé
číslo se vyskytuje nejvýše jednou, součty čísel v každémk řádku, sloupci i úhlopříčce se rovnají témuž číslu s;
např. (pro s = 15):
|
|||||||||||||||||||||||||
| Malfattiho problém | viz zde packing problem | |||||||||||||||||||||||||
| mantisa | zlomkové části logaritmů (uváděné v tabulkách); podívej charakteristika | |||||||||||||||||||||||||
| matematická analýza | zabývá se teorií reálných a komplexních čísel, diferenciálním a integrálním počtem, teorií posloupností a řad, diferenciálními rovnicemi a aplikacemi uvedených témat; základ m.a. vytvořili v 17. stol. práce Leibnize a Newtona | |||||||||||||||||||||||||
| matematická lingvistika | po 1950, Noam Chomsky; aplikovány matematické metody na zkoumání a popis abstraktních jazykových struktur, které vytvářejí ze slov gramaticky správnou větu | |||||||||||||||||||||||||
| matematická statistika | obor aplikované matematiky, který buduje teorii a metodiku získávání, zpracovávání a hodnocení hromadných dat; opírá se o počet pravděpodobnosti, teorii her a dalšími matematickými obory | |||||||||||||||||||||||||
| matematické předpony | udávají velikost daného čísla v počtech řádů pomocí specificky dané předpony; předpony jsou jak násobné tak zlomkové. více viz odkaz: PŘEDPONY | |||||||||||||||||||||||||
| matematika | řec. mathématikos - poučný; pův. se zabývala studiem čísel a
geometrických tvarů s tím, že abstrahovala postupně od měr, až vznikl pojem číslo, rozvíjela
postupy řešení zaváděním operací, rozvíjela algoritmy řešení problémů pomocí logiky a
svůj symbolický jazyk (matematika) s užitím matematických znaků více viz matematika |
|||||||||||||||||||||||||
| matice | obdélníková nebo čtvercová tabulka, v níž je zapsáno mn čísel v m řádcích a n sloupcích: (a11a21 a12a22 a13a23) kde první index vyjadřuje pořadové číslo řádku a druhý pořadové číslo sloupce; často se m. užívá v oboru geometrického zobrazování |
|||||||||||||||||||||||||
| Mayská dvacítková číselná soustava | vznikla před začátkem našeho letopočtu, ale někteří autoři ji datují až do 4. stol. př.n.l.;
vycházela asi z počítání na prtech rukou i nohou, ve které byla zhrnutá i nula; na zápis čísel používali dvě soutavy:
|
|||||||||||||||||||||||||
| medián | prostřední hodnota při uspořádání daných hodnot podle velikosti; je-li těchto hodnot sudý počet, bereme aritmetický průměr dvou prostředních hodnot | |||||||||||||||||||||||||
| Mersennova čísla | současník P.Fermata, francouzský mnich¨Martin Mersenn ve své knize 'Cogitata Physica-Mathematica' tvrdil, že čísla Mn = 2n - 1 jsou prvočísly pro n = 2,3,5,7 ... r. 1998 Roland Clarkson objevil pomocí Lucasova-Lehmerova testu prvočíslo s milionem míst: M3 021 377 |
|||||||||||||||||||||||||
| metoda Eulerových kruhů | L.Euler; způsob ověření platnosti sylogismů pomocí diagramů; spočívá ve vyjádření sylogismů třemi navzájem překrývajícími se kruhy | |||||||||||||||||||||||||
| mezikruží | jsou-li dány dva soustředné kruhy c1 a c2 takové, že poloměr kruhu c2 je větší než poloměr kruhu c1, pak množina všech bodů kruhu c2, které nejsou vnitřními body kruhu c1 se nazývá m. | |||||||||||||||||||||||||
| mimoběžky | dvě přímky v prostoru, které neleží v jedné rovině | |||||||||||||||||||||||||
| minimální plocha | matematický ekvivalent nekonečně velké mýdlové bubliny - skutečná mýdlová bublina v rámečku vytváří vždy plochu, jejíž obsah je v závislosti na tvaru rámečku minimální a matematici si zkusili představit analogii - mýdlovou bublinu, která se rozpíná do nekonečna; podobné případy byly zkoumány již konce 18. stol. a do r. 1983 byly známy pouze tři druhy podobných ploch; v dnešní době jich známe díky počítačové technice mnohem více | |||||||||||||||||||||||||
| míra | zobecnění pojmu délky, obsahu, objemu | |||||||||||||||||||||||||
| mnohohran | sjednocení všech polopřímek VX, kde X je bod ležící v daném mnohoúhelníku a V bod, který leží mimo rovinu tohoto mnohoúhelníku | |||||||||||||||||||||||||
| mnohostěn (polyedr) | geometrický útvar, který je množinou všech bodů ležících uvnitř dané mnohostěnové plochy a na této ploše;
jednoduchým m. se říka také eulerovské mnohostěny, protože pro ně platí Eulerův vzorec v + s = h + 2, kde
v, s, h jsou po řadě počty vrcholů, stěn a hran; existují i zvláštní případy m.:
|
|||||||||||||||||||||||||
| mnohostěnová plocha | geometrický útvar tvořený mnohoúhelníky (stěny) obsaženými v různých rovinách a každá strana každého z těchto mnohoúhelníků je společná dvěma mnohoúhelníkům; má-li m.p. tu vlastnost, že leží celá v jednom poloprostoru vyťatém rovinou libovolné její stěny, nazývá se konvexní | |||||||||||||||||||||||||
| mnohoúhelník | rovinný geometrický útvar; strany m. tvoří lomenou čáru a při definování m. lze také vyjít z pojmu lomené čáry; m. se nazývá pravidelný, jestliže všechny jeho strany i všechny jeho úhly jsou shodné; podle počtu stran se m. nazývá trojúhelník, čtyřúhelník, atd. | |||||||||||||||||||||||||
| množina | pojem, který matematizuje běžnou představu "souhrnu věcí"; jde o základní (nedefinovatelný) pojem; pro názornější
vysvětlení použijme slov G.Cantora, který se zasloužil o vznik teroie množin: "množina je souhrn objektů,
které jsou přesně určené a rozlišitelné a tvoří součást světa našich představ a myšlenek; tyto objekty nazýváme prvky
množiny" o prvku a množiny A se říká "a patří do množiny A" a symbolicky se zapisuje a ∈ A; jestliže prvek h nepatří do množiny A, píšeme pak h ∉ A množinu lze popsat výčtem jejich prvků, charakteristickou vlastností jejich prvků, nebo znázornit tzv. Vennovým digramem
|
|||||||||||||||||||||||||
| mocnina | m. reálného čísla a s přiozeným exponentem n je součin n činitelů rovných a; píše se an
kde a je základ mocniny, n je exponent, operace, která uspořádané dvojici (a, n) přiřazuje číslo
an se nazývá umocňování; tato definice nezahrnuje případy kdy n = 0 a n = 1, protože
součin musí mít alespoň dva činitele; klade se a0 = 1,
a1 = a s vyjímkou 00, který se nedefinuje mocnina součinu - součin čísel se umocní tak, že umocníme každého činitele a vzniklé mocniny násobíme mocnina desetinných čísel - n-tá mocnina desetinného čísla a má n-krát více desetinných čísel než číslo umocňované mocnina zlomku - ve zlomku se umocňuje čitatel i jmenovatel zvlášť mocnina záporného čísla - je-li exponent sudý, získáváme výsledek kladný a je-li exponent lichý, získáváme výsledek záporný; jestliže a>0, b je libovolné reálné číslo, pak platí ab je kladné záporný exponent - platí: a-b = 1/ab sčítání, odčítání mocnin - sčítat či odčítat smíme jen mocniny se stejnýn základem i exponentem sčítání exponentů - pro každé reálné číslo a, a každé dvě přirozená čísla m, n platí: am+n = am x an násobení, dělění mocnin - mocniny o stejném základu násobíme (dělíme) tak, že koeficinety vynásobíme (vydělíme) a společný základ umocníme součtem (rozdílem) exponentů mocnina mocniny - mocnina se umocní tak, že základ umocníme součinem exponentů druhá mocnina součtu, rozdílu - (a + b)2 = a2 + 2ab + b2; (a - b)2 = a - 2ab + b2 třetí mocnina součtu, rozdílu - (a + b)3 = a3 + 3a2 b + 3ab2 + b3; (a - b)3 = a3 - 3a2b + 3ab2 - b3 |
|||||||||||||||||||||||||
| modul | modul dané aritmetiky se nazývá číslo od něhož se opakuje číslo v tzv. konečné, resp. modulární aritmetice (viz zde) | |||||||||||||||||||||||||
| modulární aritmetika | jedná se o moderní výraz; dříve se používal termín 'konečná aritmetika'; používání početního systému, v němž se číselné hodnoty
cyklicky opakují r. 1801 K.F.Gauss ve své knize zmiňuje problém konečné aritmetiky - např. počítáme-li hodiny začneme číslem 0 a dále 1, 2, 3 ... a po čísle 11 následuje opět číslo 0 nebo počítání minut: 0, 1, 2 ... 59 a poté opět 0, proto ji pojmenoval jako 'hodinová aritmetika' |
|||||||||||||||||||||||||
| modus | hodnota, které se mezi danými hodnotami vyskytuje v největším počtu případů | |||||||||||||||||||||||||
| modus ponens | tzermín starého Řecka (stoikové); matematická logika; dedukční (odvozovací) pravidlo: jestliže platí p → q a zároveň platí p, pak platí q |
|||||||||||||||||||||||||
| Moebiův list | topologie, topologická transformace; plocha mající jen jednu stranu; pro lepší pochopení je nutno sestrojit model -
papír ve tvaru obdélníku ABCD
a slepíme strany AD a BC (list papíru "překroucený" o 180o); nyní můžeme obarvit
"obě" strany papíru aniž zvedneme tužku z papíru, resp. dokazujeme, že M.l. má jen jednu stranu zobrazení viz topologie |
|||||||||||||||||||||||||
| mohutnost množiny (kardinální číslo) |
třída množin ekvipotentních dané množině (tj. takových, že je lze vzájemně jednoznačně zobrazit na tuto množinu); je-li daná množina konečná, je její k.č. celé nezáporné číslo a je-li nekonečná, k.č. se nazývá transfinitní | |||||||||||||||||||||||||
| monom (jednočlen) | výraz, ve kterém vystupují čísla a písmena a v němž se nevyskytuje sčítání ani odčítání | |||||||||||||||||||||||||
| Möbiova páska | viz zde Moebiův list | |||||||||||||||||||||||||
| mřížové body | body, které v dané kartézské soustavě souřadnic (v rovině nebo v prostoru) mají všechny souřadnice celočíselné | |||||||||||||||||||||||||
| N | [ nahoru ] | |||||||||||||||||||||||||
| násobek | n. přirozeného čísla a je každé číslo b takové, že existuje přirozené číslo c, které splňuje rovnost b = a.c; říká se pak, že b je c-násobek čísla a; nula se pokládá za násobek každého přirozeného čísla | |||||||||||||||||||||||||
| násobení | operace, která každé uspořádané dvojici (a,b) prvků dané množiny přiřazuje prvek téže množiny, zvaný součin prvků a, b;
zapisuje se c = a x b, c = a.b nebo c = ab; prvky a,b se nazývají činitelé příslušného součinu (c); neznámého činitele
vypočteme tak, že dělíme součin známým činitelem
zákony pro násobení:
|
|||||||||||||||||||||||||
| násobnost | n. kořene a algebraické rovnice stupně n tvaru ƒ(x) = 0 je největší přirozené číslo m takové, že polynom ƒ(x) je dělitelný polynomem (x - a)m | |||||||||||||||||||||||||
| nejmenší společný jmenovatel | říkáme, že zlomky jsou uvedeny na n.s.j., jestliže mají stejný jmenovatel a ten je nejmenším společným násobkem jmenovatelů, které tyto zlomky mají po uvedení na základní tvar | |||||||||||||||||||||||||
| nejmenší společný násobek | n.s.n. několika přirozených čísel je nejmenší z jejich společných násobků; n.s.n. najdeme tak, že daná čísla rozložíme na prvočísla a potom vypočteme součin všech těchto prvočinitelů, v němž každý vystupuje pouze jednou a to s exponentem rovným největšímu exponentu, s nímž se vyskytuje v rozkladu některého z čísel; jsou-li dána čísla nesoudělná, jejich n.s.n. je roven jejich součinu | |||||||||||||||||||||||||
| největší společný dělitel | n.s.d. několika přirozených čísel je největší z jejich společných dělitelů; jsou-li dána čísla nesoudělná, jejich n.s.d. je číslo 1; užívají se dvě metody výpočtu: jednak Eukleidův algoritmus (metoda postupného dělení - viz zde); druhý způsob je rozložení každého čísla na prvočinitele a poté výpočet součinu všech těchto prvočísel, v němž každý vystupuje pouze jednou a to s exponentem rovným nejmenšímu exponentu s nímž se vyskytuje v rozkladu některého z čísel | |||||||||||||||||||||||||
| nekonečná řada | nekonečný součet, kdy součet všech nekonečně mnoha sčítanců nelze provést prostým sečtením ani je nelze všechny vypsat (1+2+3+4+ ...) | |||||||||||||||||||||||||
| nekonečno | jedná se o pomyslnou mez, nikoli řádné číslo; jakékoliv (vysoké) číslo lze navýšit o 1 a opačně, jakékoliv (malé) číslo
lze rozdělit ještě na menší díl - proto je počet čísel nekonečný; nekonečno by se mělo chápat jako vlastnost množiny čísel, nikoli jako číslo samo ∞ není číslo, ale matematický symbol (!) aritmetika, která pracuje pouze s nekonečnými čísly se nazývá transfinitní aritmetika jedna z definic nekonečna: něco, co si zachovává svoji velikost, ačkoli postupně odebíráme jednotlivé členy |
|||||||||||||||||||||||||
| nekonzistence | žádný přirozený pojem 'nekonečna' není slučitelný s pravidly aritmetiky: Ox = 1, pak by x = ∞ a tato rovnice vede k n. | |||||||||||||||||||||||||
| nepřímá úměrnost | dvě veličiny jsou nepřímo úměrné tehdy, jestliže jedna veličina v určitém poměru vzroste a druhá v témže poměru klesne kolikrát se zmenší jedna veličina, tolikrát se zvětší druhá veličina; kolikrát se zvětší jedna veličina, tolikrát se zmenší druhá veličina |
|||||||||||||||||||||||||
| nerovnice | úkol najít všechna čísla (z dané množiny), pro která platí daná nerovnost; tato čísla tvoří řešení nerovnice | |||||||||||||||||||||||||
| nerovnost | relace, která vyjadřuje uspořádání čísel podle velikosti | |||||||||||||||||||||||||
| nespojitost funkce | funkce y = ƒ(x) je nespojitá v bodě x0, jestliže v tomto bodě není spojitá; může to nastat, např. jestliže limita ƒ(x) pro x → x0 existuje, ale není rovna ƒ(x0), nebo jestliže existují limity zprava a zleva pro x → x0, ale nejsou si rovny (bod nespojitosti prvního druhu), nebo jestliže z těchto limit existuje pouze jedna nebo žádná (bod nespojitosti druhého druhu) | |||||||||||||||||||||||||
| neurčitá úloha | úloha, která má nekonečně mnoho řešení | |||||||||||||||||||||||||
| nevlastní prvek | pojem užívaný v projektivní geometrii, kde se zkoumá projektivní rovina; v této rovině se dvě různé přímky vždy protínají, protože dvě rovnoběžné přímky se protínají v tzv. nevlastním bodě (pro představu bod v nekonečnu) | |||||||||||||||||||||||||
| nomografie | grafické znázorňování funkcí několika proměnných pomocí soustavy kótovaných čar a bodů, tzv. nomogramů | |||||||||||||||||||||||||
| normála | kolmice k tečně křivky c procházející jejím bodem dotyku P nebo kolmice k tečně rovině plochy δ procházející jejím bodem dotyku P | |||||||||||||||||||||||||
| nula | jakožto přirozené číslo je to počet prvků prázdné množiny, to je kardinální číslo vyjádřené jako třída prázdných množin | |||||||||||||||||||||||||
| O | [ nahoru ] | |||||||||||||||||||||||||
| obálka | křivka určená svými tečnami | |||||||||||||||||||||||||
| objem | číslo udávající prostorovou velikost tělesa v určitých jenotkách; jednotkou objemu je objem krychle, jejíž hrana je jednotkou délky; více viz vzorce pro výpočet objemu některých těles | |||||||||||||||||||||||||
| oblouk | množina bodů křivky mezi dvěma jejími body A a B | |||||||||||||||||||||||||
| obsah | číslo udávající plošnou velikost obrazce v rovině nebo plochy v prostoru v určitých jednotkách; jednotkou obsahu je čtverec, jehož strana je jednotkou délky; více viz vzorce pro výpočet obsahu některých obrazců | |||||||||||||||||||||||||
| odčítání | obrácený početní výkon ke sčítání (viz zde) na množině přirozených čísel je to operace, která každé uspořádané dvojici (a,b), kde a ≥ b, přiřazuje přirozené číslo c takové, že a = b + c, resp. a - b = c; čísla a, b, c se nazývají po řadě menšenec, menšitel a rozdíl dle předchozího zápisu: menšenec se rovná součtu menšitele a rozdílu |
|||||||||||||||||||||||||
| odchylka |
|
|||||||||||||||||||||||||
| odmocnina | je-li n přirozené číslo, pak n-tá odmocnina z nezáporného reálného čísla a je nezáporné reálné číslo q, pro něž
qn = a; píšeme q = n√a nebo q = a1/n;
číslo n se nazývá odmocnitel, číslo a odmocněnec odmocnina součinu - součin se odmocňuje tak, že odmocníme každého činitele a vzniklá čísla znásobíme odmocnina zlomku - zlomek se odmocňuje tak, že odmocníme čitatele i jmenovatele |
|||||||||||||||||||||||||
| odvěsna | viz trojúhelník | |||||||||||||||||||||||||
| ordinalita | pořadí čísla v posloupnosti (srovnej: kardinalita) též viz odkaz ČÍSLA, přirozená čísla |
|||||||||||||||||||||||||
| ortocentrum | průsečík všech tří výšek trojúhelníku | |||||||||||||||||||||||||
| oskulační |
|
|||||||||||||||||||||||||
| ovál | rovinná uzavřená křivka, která má tu vlastnost, že je-li t její libovolná tečna, pak všechny body této křivky
náležejí jedné z polorovin vyťatých přímkou t Descartesův ovál - množina bodů P v rovině takových, že platí m.PA + n.PB = k, kde A, B jsou dva pevné body v rovině a k, m,n kladné reálné konstanty; je-li m = n = 1, pak D.o. je elipsa |
|||||||||||||||||||||||||
| P | [ nahoru ] | |||||||||||||||||||||||||
| packing problem | též problém optimálního zabalení či Malfattiho problém; úkolem je vepsat do trojúhelníku tři nepřekrývající se kruhy, aby jejich celkový obsah
byl co největší (souvisí s problémem optimálního balení pomerančů); formulován r. 1803 (Malfatti) a řešení znělo: kruhy zvolíme tak, aby
se každý dotýkal dvou stran trojúhelníku a obou zbývajících kruhů (obr. 1); r. 1930 bylo Mafattiho řešení poznáno jako špatné pro případ
rovnostranného trojúhelníku - je nutno nejprve vepsat největší možný kruh a pak doplnit dva menší (obr. 2, 3); r. 1965 byla opět odhalena
nesprávnost Malfattiho řešení pro dlouhé a úzké trojúhelníky (obr. 4, 5); konečně r. 1967 ukázal M.Goldberg, že Malfattiho řešení není
správné nikdy - správně je vždy pouze, když se jeden z kruhů dotýká všech stran trojúhelníku a poté se dopíší dva zbývající kruhy (obr. 6, 7) obrázky 1-7 |
|||||||||||||||||||||||||
| Pappovy věty | vztahují se k tělesům vzniklým rotací rovinného obrazce kolem přímky, která neprochází jeho vnitřkem; tvrdí:
|
|||||||||||||||||||||||||
| parabola | kuželosečka, množina bodů P v rovině, jejichž vdálenost od daného pevného bodu F (zvaného ohnisko) v této
rovině je rovna jejich vzdálenosti od pevné přímky d (zvaná řídící přímka) rovněž v této rovině, která neprochází
bodem F obecná rovnice paraboly: y = ax2 + bx + c |
|||||||||||||||||||||||||
| paraboloid (rotační) | plocha vytvořená rotací paraboly kolem její osy | |||||||||||||||||||||||||
| paradox | tvrzení, které je v rozporu se "zdravým rozumem", tj. způsobem myšlení založeným na určitých myšlenkových
návycích, zdánlivě protismyslné tvrzení nebo jev např. zde (paradox) Achilles a želva |
|||||||||||||||||||||||||
| parametr | termín, kterým se označují proměnné číselné hodnoty, které se objevují v rovnici jako koeficienty u neznámých | |||||||||||||||||||||||||
| paralaxa | úhel mezi dvěma myšlenými přímkami vedenými k témuž objektu ze dvou různých pozorovacích míst. Trigonometrická paralaxa - paralaxa určená trigonometrickou metodou, tj. na základě měření dvou úhlů na obou koncích zvolené základny; základnou může být např. poloměr zemské trajektorie (roční paralaxa) nebo poloměr Země (denní, horizontální paralaxa) | |||||||||||||||||||||||||
| parciální derivace | funkce o více proměnných je její derivace vzhledem k jedné z těchto proměnných,
přičemž s ostatními proměnnými zacházíme jako s konstantami využívají se např. ve vektorovém počtu či v diferenciální geometrii typickým příkladem parciálních diferenciálních rovnic jsou Maxwellovy rovnice |
|||||||||||||||||||||||||
| Pascalova věta | projektivní geometrie, B.Pascal; P.v. tvrdí: zvolíme-li šest bodů A1, ..., A6 na kuželosčce, pak průsečíky přímek A1A2 a A4A5 ad. leží v jedné přímce "jesltiže vrcholy šestiúhelníku leží střídavě na dvou různých přímkách, pak body, ve kterých se protínají protilehlé strany, leží na jedné přímce" |
|||||||||||||||||||||||||
| pentagon pentagram |
tzv. posvátné geometrickém obrazce - mystický symbol Pythagorejců; více viz pentagram | |||||||||||||||||||||||||
| permutace | vzájemně jednoznačné zobrazení množiny na sebe; počet všech p. n-prvkové množiny je n!, kde vykřičník je faktoriál (viz zde) | |||||||||||||||||||||||||
| pí (π) | π = 3,14159 26535 8979... nejjednodušší definica čísla pí: obvod kružnice je přímo úměrný jejímu průměru (obvod : průměr) a tento podíl bude roven nějakému číslu, které bude stejné pro všechny kružnice a toto číslo označme symbolem π také viz stručná historie čísla pí |
|||||||||||||||||||||||||
| planimetrie | geometrie v rovině | |||||||||||||||||||||||||
| plášť | u hranolu, jehlanu, komolého jehlanu, válce, kužele a komolého kužele a kulové vrstvy označuje povrch tělesa s výjimkou podstav | |||||||||||||||||||||||||
| Playfairův postulát | danou přímkou a bodem, který na ní neleží, lze vést právě jednu rovnoběžku s danou přímkou (formální definice "rovnoběžnosti" říká, že dvě přímky jsou rovnoběžné, jestliže se při žádném prodloužení neprotnou - jedná se fakticky o ekvivalentní vyjádření k původní Eukleidově formulaci, pátému postulátu rovnoběžnosti) |
|||||||||||||||||||||||||
| plocha | Eukleidés rozuměl plochou "to, co má jen šířku a délku" a vystihuje tak jejich dvojrozměrnost běžné plochy lze získat "spojitou deformací" kruhu nebo kulové plochy analytické definice charakterizují plochu jako množinu všech bodů prostoru, jejichž souřadnice [x,y,z] splňují rovnici typu F(x,y,z) = 0 (implicitní rovnice p.), z = ƒ(x,y) (explicitní rovnice p.) pět základních vlastností plochy:
|
|||||||||||||||||||||||||
| PNT | viz zde "první věta o prvočíslech" | |||||||||||||||||||||||||
| početní systém | k běřným matematickým úkolům se užívá desítkový početní systém, resp. desítková soustava, tj. čísla 0 - 9 např. kmen Vedda (Srí Lanka) užívá "pouze" jedničkový početní systém a to tak, že chce-li spočítat třeba kokosové ořechy, vezme hůlku a položí ji k prvnímu ořechu a dále pokračuje postupným přikládáním hůlek k dalším ořechům a vždy řekne "to je jeden"; když by chtěl pozorovatel užívající desítkovou soustavu vědět celkový počet (součet), pak by příslušník kmene Vedda ukázal na hromadu hůlek a řekne: "tolik" |
|||||||||||||||||||||||||
| podmnožina | p. množiny A je libovolná množina B, která obsahuje jen prvky patřící do A; značí se B ⊂ A | |||||||||||||||||||||||||
| Poincarého hypotéza (domněnka) | topologie; problém teorie variet, přesněji řečeno jejich klasifikace, a to pro třírozměrné variety více viz problémy tisíciletí |
|||||||||||||||||||||||||
| pól | základní bod polární soustavy souřadnic; pól v projektivní geometrii - viz polára | |||||||||||||||||||||||||
| polára | pojem projektivní geometrie; vedeme-li bodem P přímku, která protíná kuželosečku ve dvou bodech A a B, a uvažujeme-li bod P´ takový, aby čtveřice (PP´AB) byla harmonická, lze dokázat, že při změně přímky procházející bodem P se mění i bod P´, ale leží vždy na téže přímce, která se nazývá p. bodu P vzhledem k uvažované kuželosečce | |||||||||||||||||||||||||
| poloprostor | rovina α určuje v prostoru dvě množiny bodů; body každé z nich leží na téže straně od roviny α každá z těchto množin se nazývá vnitřek poloprostoru s hraniční rovinou α | |||||||||||||||||||||||||
| polopřímka | bod O rozděluje přímku r na dvě části tak, že body každé z nich leží na téže straně od bodu O; každá z těchto množin se nazývá vnitřek polopřímky s počátkem O | |||||||||||||||||||||||||
| polorovina | přímka r v rovině určuje v této rovině dvě množiny bodů; body každé z těchto množin leží na stejné straně od přímky r; každá z těchto množin se nazývá vnitřek poloroviny o hraniční přímce r | |||||||||||||||||||||||||
| polynom | neboli mnohočlen; jedná se o výraz typu a0xn + a1xn-1 + a2xn-2 + ... + an-1x + an kde koeficienty a0, a1, a2, ... an jsou prvky množiny A a x je proměnná nabývající hodnot z množiny A |
|||||||||||||||||||||||||
| poĺytyp | viz zde 'simplexová metoda' | |||||||||||||||||||||||||
| poměr | poměr dvou čísel zapisujeme a:b; vyjadřujeme jím srovnání dvou čísel; s poměrem dvou čísel se často ztotožňuje jejich podíl | |||||||||||||||||||||||||
| pořadí | p. daných n prvků, jakékoliv rozmístění těchto n prvků za sebou, uspořádaná n-tice obsahující každý prvek právě jednou | |||||||||||||||||||||||||
| posloupnost | p. prvků množiny A je funkce, která každému přirozenému číslu přiřazuje prvek množiny A; obvykle se zapisuje
a1, a2, a3, ..., které tato
funkce přiřazuje číslům 1, 2, 3
|
|||||||||||||||||||||||||
| postulát stejné vzdálenosti | rovnoběžky jsou všude stejně vzdáleny (jedná se fakticky o ekvivalentní vyjádření k původní Eukleidově formulaci, pátému postulátu rovnoběžnosti) |
|||||||||||||||||||||||||
| pravděpodobnost | míra možnosti, že se daný jev uskuteční; matematická hodnota p. nabývá hodnoty mezi 0 a 1, resp. udává se v procentech | |||||||||||||||||||||||||
| pravdivostní hodnoty | logika; hodnoty, kterých může nabývat výroková funkce; nabývá hodnot 0 (nepravda) a 1 (pravda) | |||||||||||||||||||||||||
| predikát | (matematická logika) jazykové sdělení (výraz), o němž má po obsahové stránce smysl tvrdit, že je buď pravdivé (true - 1), nebo nepravdivé (false - 0) | |||||||||||||||||||||||||
| predikátová logika | odvozovací systém používaný k popisu matematických teorií a vět; je rozšířením výrokové logiky (bohatší vyjadřovací schopnost) | |||||||||||||||||||||||||
| premisa | (matematická logika) lat. praemittere = napřed posílat, předesílat; p. označuje předpoklad; premisa je výrok, jenž je součástí logického soudu a logickým postupem lze určit, zda souhrn premis zahrnuje určitý závěr | |||||||||||||||||||||||||
| primitivní funkce | viz integrál | |||||||||||||||||||||||||
| princip duality | projektivní geometrie (viz zde); vyplývá ze symetrie obsažené v axiomech projektivní geometrie při zahrnutí ideálních bodů a
ideálních přímek; p.d. zní: když se v libovolné větě navzájem zamění pojmy 'bod' a 'přímka' nebo slovní spojení 'body ležící na stejné přímce' a 'přímky protínající se v jediném bodě', pak výsledkem bude platná věta, která se nazývá "věta duální" |
|||||||||||||||||||||||||
| prizmatoid (hranolec) | mnohostěn, jehož vrcholy jsou vrcholy dvou mnohoúhelníků, zvaných podstavy, které leží v rovnoběžných rovinách a jehož stěny jsou kromě těchto dvou podstav trojúhelníky a lichoběžníky | |||||||||||||||||||||||||
| problémy tisíciletí | 24.5.2000 vyhlásili matematikové M.Atiyah a J.Tate, že bude vyplacen jeden milión amerických dolarů osobě nebo osobám,
které nebo kteří jako první vyřeší kterýkoliv ze sedmi nejtěžších matematických problémů; tuto částku (7 000 000 $) poskytl
obdivovatel matematiky (a majitel investičních fondů) Landon Clay, kdy rok před tím založil v Cambridge (Massachusetts) Clayův
matematický institut (CMI) podrobněji pod odkazem: problémy tisíciletí a též zde: Hilbertovy problémy |
|||||||||||||||||||||||||
| procento | procento (1%) z daného čísla znamená setinu (1/100) z tohoto čísla; názvy související: základ, procentová část a počet procent: je-li počet procent 100 je procentová část rovna základu | |||||||||||||||||||||||||
| projektivní geometrie | obor geometrie, který zkoumá projektivní zobrazení (kolineace), to je taková vzájemně jednoznačná zobrazení,
která danému geometrickému útvaru přiřazují útvar, který z něho vznikne konečným počtem promítání (např. v malířství
znázorňuje vícebodovou perspektivu) axiomatizace projektivní geometrie:
|
|||||||||||||||||||||||||
| Proklusův axiom | jestliže přímka protíná jednu ze dvou rovnoběžek, pak musí protínat také druhou rovnoběžku (jedná se fakticky o ekvivalentní vyjádření k původní Eukleidově formulaci, pátému postulátu rovnoběžnosti) |
|||||||||||||||||||||||||
| proměnná | symbol, nejčastěji písmeno, které nahrazuje libovolný prvek z nějaké množiny, tzv. oboru proměnných; např.: funkce y = ƒ(x); x se nazývá nezávisle proměnná a y závisle proměnná, protože její hodnota závisí na p. x | |||||||||||||||||||||||||
| promile | promile (1‰) z daného čísla znamená tisícinu (1/1000) z tohoto čísla | |||||||||||||||||||||||||
| průměr |
|
|||||||||||||||||||||||||
| první věta o prvočíslech | též PNT či prvočíselná věta; více viz zde | |||||||||||||||||||||||||
| prvočíslo | každé přirozené číslo a, které má právě dva kladné dělitele, a to sebe samo a 1 (2, 3, 5, 7, 11, 13 ...) více viz zde |
|||||||||||||||||||||||||
| přátelská čísla | objevily je Pythagorejci; dvě čísla jsou přátelská, jestliže součet dělitelů prvního čísla je roven číslu druhému a vice versa; např. p.č. jsou 220 a 284; 220 je dělitelné čísly 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 a 110: součet těchto dělitelů dává číslo 284, které je dělitelné právě čísly 1, 2, 4, 71 a 142, které v součtu dávají číslo 220; dnes je p.č. známo přes tisíc (např.: 1184 - 1210; 2620 - 2924; ... 10 744 - 10 856 ad.) | |||||||||||||||||||||||||
| přímá úměrnost | dvě veličiny jsou přímo úměrné tehdy, jestliže se obě veličiny v témže poměru zvětšují nebo zmenšují kolikrát se zmenší jedna veličina, tolikrát se zmenší druhá veličina; kolikrát se zvětší jedna veličina, tolikrát se zvětší druhá veličina |
|||||||||||||||||||||||||
| přímka | základní geometrický pojem; Eukleides ji charakterizoval tím, že má jen délku; je popsána soustavou axiomů, jako např.: ke každým dvěma různým bodům roviny existuje právě jedna přímka každá přímka obsahuje alespoň tři body ke každé přímce existuje alespoň jeden bod, který v ní není obsažen ad.
|
|||||||||||||||||||||||||
| přirozené číslo | celá čísla 1, 2, 3 ...; p.č. popisují strukturu souboru (např. předmětů); struktury vyjádřené čísly jsou abstraktní a stejně tak jsou abstraktní čísla, které je popisují; více čísla | |||||||||||||||||||||||||
| přirozený logaritmus | zn. 'ln'; logaritmická funkce o základu 'e' (Eulerovo číslo); funkce přirozeného logaritmu: logex = ln x funkce byla objevena na poč. 19. století a její definice vychází z analýzy nekonečného procesu a tvoří součást disciplíny 'vyšší kalkulus' nebo 'reálná analýza'; jedná se o inverzní funkci k funkci exponencilání ex. Grafem funkce je hladká spojitá křivka |
|||||||||||||||||||||||||
| půlkruh | jedna ze dvou částí, na které libovolný průměr kruhu dělí kruh | |||||||||||||||||||||||||
| půlkružnice | jedna ze dvou částí, na které libovolný průměr kružnice dělí kružnici | |||||||||||||||||||||||||
| Pýthagorova věta | byla známa již dávno před Pythagorovým narozením ... už Egypťané ve svých učebnicích radili jak sestrojit při měření pravý úhel: "Nanes na jeden provazec tři, na druhý čtyři díly a vzdálenost mezi takto vzniklými body nechť je pět dílů. Pak je úhel pravý." Podle této poučky je možno vytyčit pravý úhel i za pomoci libovolných čísel. Řekové pak konstatovali, že v pravoúhlém trojúhelníku je součet čtverců nad odvěsnami roven čtverci nad přeponou: a2 = b2 + c2 |
|||||||||||||||||||||||||
| R | [ nahoru ] | |||||||||||||||||||||||||
| racionální číslo | řec. ratio = poměr; moderní termín r.č., tj. číslo, které lze vyjádřit jako podíl (poměr) dvou celých čísel; řecký pojem
čísla byl těsně svázán s geometrií a čísla byla chápána jako délkové a plošné míry - výsledky měření různých úhlů, délek
a ploch, které bychom mohli vyjádřit pomocí celých čísel a zlomků, Řekové udávali vzájemným provnáním (poměřováním) dvou
různých úhlů, délek či ploch více viz čísla |
|||||||||||||||||||||||||
| radián | jednotka velikosti úhlu; jeden radián je velikost středového úhlu kružnice příslušejícího oblouku, jehož délka je rovna poloměru kružnice; přímý úhel má velikost π radiánů (délka půlkružnice o poloměru r je πr); 1 rad = 57o 17´ 44´´ | |||||||||||||||||||||||||
| Rámanudžanova konstanta | tato konstanta fakticky neexistuje ... jedná se vlastně o aprílový žert z časopisu Scientific American, kde bylo předloženo, že indický matematik Rámanudžan dokázal tvrzení Charlese Hermiteho z r. 1859, že hodnota čísla exp{π(163)1/2} je celé číslo; je to však jen tzv. "numerická shoda" a hodnota je opravdu blízká celému číslu: 262 537 412 640 768 743, 999 999 999 999 25... | |||||||||||||||||||||||||
| reciproké prvky | též inverzní p.; každé dva prvky množiny A, na níž je definována operace zvaná násobení, které má neutrální prvek, jestliže součin těchto prvků je roven neutrálnímu prvku | |||||||||||||||||||||||||
| reductio ad absurdum | tzv. "nepřímá" metoda důkazu; řetězec úvah, kterým dokážeme nějaké tvrzení (důkaz sporem); r. 1736 L.Euler pomocí této metody řešil problém tzv. Královeckých mostů (více zde) | |||||||||||||||||||||||||
| reduplikace krychle | viz Délský problém (zde) | |||||||||||||||||||||||||
| reflexivita | viz relace (zde) | |||||||||||||||||||||||||
| rechenbank | něm. výpočetní lavice; z tohoto slova vzniklo i slovo 'banka'; do 13. stol. se počtáři peněz museli spokojit s abakem nebo různými početními destičkami, které Němci nazývali právě 'rechenbank' - bankéři je potřebovali k zaznamnávání půjček: jednalo se o kontrolní trámky, na jejichž boční straně byla vyznačena peněžní hodnota a pak byl trámek podélně rozštípnut na dva stejné díly a bankéř si ponechal jeden kus, základ dřevěného trámku, který nesl označení 'stock' (v angl. znamená slovo 'stock' mj. také akcii; Anglická státní banka vedla účty do r. 1826 pomocí různých kontrolních trámků - r. 1834 byly spáleny v kamnech Horní sněmovny a od kamen přehlcenými těmito kusy dřeva se vznítilo celé obložení a z něj se poté oheň rozšířil na celou Horní sněmovnu, z níž pak nakonec zbyl jen popel ...) | |||||||||||||||||||||||||
| rektifikace | konstrukce úsečky, jejíž délka je rovna délce dané křivky c; je-li možno provésr r. euklidovsky (jen s pomocí pravítka a kružítka), křivka c se nazývá rektifikovatelná | |||||||||||||||||||||||||
| relace | binární relace na množině A je podmnožina kartézského součinu A x A, tj. množina uspořádaných dvojic, jejichž
prvky patří do množiny A; r. je určena, je-li známo kritérium, podle něhož jsou uspořádané dvojice vybrány, nebo výčet
těchto dvojic
|
|||||||||||||||||||||||||
| Rhindův papyrus | první početní tabulky ze 17. stol. př.n.l. (Egypt) | |||||||||||||||||||||||||
| riemannovská geometrie | v prostoru je součet úhlů v trojúhelníku vždy vyšší než 180o; prostor je neeuklidovský; daným bodem v prostoru nelze vést ani jednu rovnoběžku k dané přímce | |||||||||||||||||||||||||
| rombododekaedr | mnohostěn, jehož stěny tvoří dvanáct kosočtverců | |||||||||||||||||||||||||
| romboedr | též klenec; mnohostěn, jehož stěny jsou shodné kosočtverce | |||||||||||||||||||||||||
| rotační tělesa | tělesa vytvořená rotací rovinné oblasti omezené uzavřenou křivkou kolem pevné přímky | |||||||||||||||||||||||||
| rovina | základní geometrický pojem; Eukleidés jí charakterizoval tím, že má jen délku a šířku; je popsána soustavou axiómů, např.: k libovolným třem bodům roviny neležícím v přímce existuje právě jedna rovina, která je obsahuje ke každé rovině existuje bod, který v ní neleží leží-li dva různé body přímky v rovině, pak celá přímka leží v této rovině ad. |
|||||||||||||||||||||||||
| rovinný pás | průnik dvou polorovin, jejichž hraniční přímky jsou spolu rovnoběžné a z nichž každá obsahuje hraniční přímku druhé | |||||||||||||||||||||||||
| rovnice | úloha najít všechny prvky z dané množiny, pro které platí daná rovnost, dosadíme-li je za neznámou - každý takový prvek a proces jeho hledání je řešení rovnice; více o typech rovnic: ROVNICE | |||||||||||||||||||||||||
| rovnoběžky | rovnoběžné přímky; dvě přímky ležící v téže rovině se nazývají rovnoběžné, jestliže buď splývají, nebo jejich průnik je prázdný | |||||||||||||||||||||||||
| rovnoběžné roviny | dvě roviny, které buď splývají, nebo jejich průnik je prázdný | |||||||||||||||||||||||||
| rovnost | r. dvou množin A, B znamená, že se obě skládajíá z týchž členů | |||||||||||||||||||||||||
| rozdíl | viz odčítání (zde) | |||||||||||||||||||||||||
| různoběžky | různoběžnjé přímky; dvě přímky, které mají právě jeden společný bod; k libovolným dvěma r. existuje právě jedna rovina, která je obě obsahuje | |||||||||||||||||||||||||
| řada | nekonečná řada; součet nekonečně mnoha sčítanců; řada se zkráceně označuje pomocí sumačního znaménka Σ;
řada může být konvergentní nebo divergentní (dle posloupnosti částečných součtů) dlouhý zápis součtu typu a1 + ... an se zkracuje s použitím symbolu 'sumy' 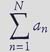 , kde 'n' je sčítací index, který probíhá mezi dvěma vyznačenými hodnotami,
v tomto případě mez 1 a N
geometrická řada (v níž a1, a2,
a3, ... tvoří geometrickou posloupnost) je konvergentní, právě když absolutní hodnota
kvocientu příslušné g.ř. je menší než 1; potom součet řady je a1/(1-q),
kde q je kvocient , kde 'n' je sčítací index, který probíhá mezi dvěma vyznačenými hodnotami,
v tomto případě mez 1 a N
geometrická řada (v níž a1, a2,
a3, ... tvoří geometrickou posloupnost) je konvergentní, právě když absolutní hodnota
kvocientu příslušné g.ř. je menší než 1; potom součet řady je a1/(1-q),
kde q je kvocient
|
|||||||||||||||||||||||||
| řetězovka | viz KATENOIDA | |||||||||||||||||||||||||
| řez | řez tělesa nebo plochy rovinou, průnik s touto rovinou, tzv. rovinou řezu | |||||||||||||||||||||||||
| římské číslice | 1 = I; 5 = V; 10 = X; 50 = L; 100 = C; 500 = D; 1000 = M II = 2 (1+1); IV = 4 (5-1); VIII = 8 (5+3); IX = 9 (10-1) ... XXIX = 29 (20+9) ... MCM = 1900 (1000+900) |
|||||||||||||||||||||||||
| S | [ nahoru ] | |||||||||||||||||||||||||
| samodružné prvky | s.p. geometrického zobrazení jsou takové prvky, které v tomto zobrazení odpovídají samy sobě | |||||||||||||||||||||||||
| sčítání | s. v dané množině A čísel nebo veličin je operace, která každé uspořádané dvojici (a, b) prvků množiny A
přiřazuje prvek c množiny A zvaný součet prvků a, b; píše se a + b = c, prvky a, b se nazývají sčítance; c se nazývá součet
zákony pro sčítání:
|
|||||||||||||||||||||||||
| sečna | s. křivky je přímka, která má s křivkou společné alespoň dva různé body | |||||||||||||||||||||||||
| sférický trojúhelník | na kulové ploše je určen oblouky hlavních kružnic, z nichž jeden jde z bodu A do bodu B, druhý z bodu B do bodu C, třetí z bodu C do bodu A, kde A, B, C jsou body kulové plochy | |||||||||||||||||||||||||
| shodnost | s. dvou geometrických útvarů je názorný pojem; např. je-li možno jeden z útvarů přemístit tak, aby splynul s druhým, jsou útvary shodné | |||||||||||||||||||||||||
| simplexová metoda | matematické zkoumání útvarů ve čtvrtém a vyšším rozměru je založeno na s.m., která poskytuje řešení prostřednictvím vícerozměrné geomatrie - celý proces je vyjádřen geometrickým útvarem v n-rozměrném prostoru, kde 'n' udává počet nezávislých parametrů; v typickém případě bude tento útvar vypadat jako n-rozměrná verze mnohostěnu - tyto útvary se nazývají "polytytpy" | |||||||||||||||||||||||||
| singularity | body v nichž funkce tzv. "exploduje"; před Riemannem by funkce 1/x byla zcela neřešitelná, protože blíží-li se 'x' zprava k nule, výraz 1/x se stává větším a větším až se funkce v nule "přetrhne" a zanikne v nekonečnu | |||||||||||||||||||||||||
| skalár | skalární veličina; veličina jejíž hodnoty jsou dány jediným číslem, tzv. číselnou hodnotou skalární veličiny a příslušnou měřící jednotkou (např. hmotnost je definována jediným číslem, resp. veličinou - kilogramem, narozdíl např. od rychlosti, která je definována jako podíl dráhy a času, tedy dvou veličin) | |||||||||||||||||||||||||
| soroban | japonská obdoba suan-pan (počítadlo nebo-li abacus) | |||||||||||||||||||||||||
| součet | viz 'suma' (zde) | |||||||||||||||||||||||||
| součin | dlouhý zápis součinu typu a1 x ... an se zkracuje s použitím symbolu 'součinu'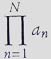 , kde 'n' je násobící index, který probíhá mezi dvěma vyznačenými hodnotami,
v tomto případě mez 1 a N , kde 'n' je násobící index, který probíhá mezi dvěma vyznačenými hodnotami,
v tomto případě mez 1 a N
|
|||||||||||||||||||||||||
| souměrnost | obrazec má střed souměnrosti (je středově souměrný), jestliže existuje středová souměrnost, která je převádí v sebe sama | |||||||||||||||||||||||||
| souřadnice | obecně, jedná se o čísla, která určují polohu bodu na přímce, v rovině nebo v prostoru; soustava souřadnic je vzájemně jednoznačné zobrazení mezi množinou bodů přímky (resp. roviny či prostoru) a množinou čísel (resp. uspořádaných dvojic či trojic čísel), která představují souřadnice těchto bodů; rozlišujeme: afinní (lineární) souřadnice v rovině, kartézské souřadnice v rovině, kartézské souřadnice v prostoru, cylindrické souřadnice, polární souřadnice v rovině, souřadnice bodu na kulové ploše a sférické souřadnice | |||||||||||||||||||||||||
| soustava rovnic | s.r. je tvořena dvěma nebo více rovnicemi o dvou nebo více neznámých, od nichž se požaduje, aby byly splněny současně | |||||||||||||||||||||||||
| spirály | křivky definované kinematicky jako trajektorie bodů, které se pohybují po přímce podle daného pravidla,
zatímco přímka rotuje konstantní rychlostí kolem daného pevného bodu
|
|||||||||||||||||||||||||
| spočetná množina | je to taková množina, že existuje vzájemně jednoznačné zobrazení mezi touto množinou a množinou všech přirozených čísel | |||||||||||||||||||||||||
| spojitost | intuitivně je spojité to, co nemá "díry"; taková je například úsečka, přímka či rovina | |||||||||||||||||||||||||
| spojitost funkce | definice: funkce ƒ(x) je spojitá v bodě c, kde c je bod definičního oboru této funkce, jestliže její limita pro x → c je rovna hodnotě této funkce v bodě c; funkce je spojitá v intervalu patřícím do jejího definičního oboru, jestliže je spojitá v každém bodě tohoto intervalu | |||||||||||||||||||||||||
| spor | ve sporu jsou dvě podmínky, které nemohou být splněny současně; například podmínky a > b a současně a < b | |||||||||||||||||||||||||
| standardní plocha | topologie; určitý typ povrchu, jimiž lze charakterizovat všechny povrchy | |||||||||||||||||||||||||
| stereometrie | prostorová geometrie | |||||||||||||||||||||||||
| stíhací křivka | trajektorie bodu, který se z dané počáteční polohy pohybuje rychlostí konstantní velikosti stále směrem k jinému bodu, který se pohybuje rovnoměrným přímočarým pohybem | |||||||||||||||||||||||||
| stock | viz zde 'rechenbank' | |||||||||||||||||||||||||
| strana | u mnohoúhelníku úsečka spojující dva jeho sousední vrcholy nebo její délka; v projektivní geometrii např. každá z přímek tvořících čtyřstran | |||||||||||||||||||||||||
| struktura | algebraická struktura je objekt tvořený množinou a alespoň jednou operací definovanou na této množině; je-li tato množina A a operace je *, struktura se symbolicky značí (A, *) | |||||||||||||||||||||||||
| střední hodnota funkce | s.h.f. ƒ(x), která je definována na intervalu <a, b> a z níž existuje integrál přes tento
interval, je rovna [1/(b-a)][∫abƒ(x)dx] - (viz určitý integrál) |
|||||||||||||||||||||||||
| stupeň | jednotka velikosti úhlu; jedna devadesátina pravého úhlu; odvozené jednotky jsou dále úhlová minuta a úhlová vteřina
|
|||||||||||||||||||||||||
| suan-pan | bambusové hůlky na nichž jsou navlečeny jádra: první počítadlo; cca 5000 let př.n.l., Čína (počítadlo nebo-li abacus) | |||||||||||||||||||||||||
| subnormála | je-li dána rovinná křivka c, její tečna t v bodě P, její normála n v bodě P a přímka r, pak subnormála křivky c v bodě P na přímce r je úsečka QN, kde Q je pravoúhlý průmět bodu P na přímku r a N je průsečík přímek n a r | |||||||||||||||||||||||||
| sugestivní čísla | pracují s nimi především numerologové a nemají žádné opodstatnění v aplikované matematice např. tzv. apokalyptické číslo (viz zde) |
|||||||||||||||||||||||||
| Suisethova posloupnost | též Suisethova sekvence; R.Suiseth; sečtením nekonečného počtu členů se získá konečný výsledek:
1/2 + 2/4 + 3/8 + 4/16 ... + n/2n = 2 tento trik - sečtení nekonečného počtu členů pro získání konečného výsledku - učinil na základě skoro 2000 let starého tzv. paradoxu o Achillovi a želvě (viz zde) |
|||||||||||||||||||||||||
| suma | nebo též sumační znaménko; viz řada (zde) | |||||||||||||||||||||||||
| svaz | uspořádaná množina, v níž ke každm dvěma prvkům x, y existuje nejmenší prvek, který je větší nebo roven x i y a největší prvek, který je menší nebo roven x i y | |||||||||||||||||||||||||
| sylogismus | (matematická logika) s. = rozhodnutí, logický důsledek; druh logického tvrzení, ve kterém je jeden z výroků odvozen z ostatních dvou předpokladů - premis (viz zde) | |||||||||||||||||||||||||
| symetrie | s. se zkoumá prostřednictvím transformace (viz zde) objektů - posunutí, zvětšování, aj. symetrií nějakého útvaru nazýváme takovou transformaci, která ponechá objekt nezměněný (např. kruh)
|
|||||||||||||||||||||||||
| šroubovice | trajektorie bodu ležícího na rotační válcové ploše, který vykonává současně dva pohyby: rovnoměrný rotační pohyb kolem osy válcové plochy a rovnoměrný přímočarý pohyb po tvořící přímce válcové plochy | |||||||||||||||||||||||||
| T | [ nahoru ] | |||||||||||||||||||||||||
| tajemná rovnice | rovnice x2 + 1 = 0 nemá žádné reálné řešení a proto byla pro matematiky dlouho tajemná Až v r. 1830 C.F.Gauss dal této rovnici geometrický tvar a spojil tak čísla reálná s komplexními veličinami, totiž: eiπ + 1 = 0 dnes se jedná o jednu z nejslavnějších rovnic |
|||||||||||||||||||||||||
| Tanijamova-Šimurova domněnka | spojuje eliptické křivky a modulární formy, což jsou dvě odvětví matematiky s naprosto různými principy a přístupy k problémům, avšak při bližším pohledu vykazují mnohé spojitosti a společné vlastnosti | |||||||||||||||||||||||||
| Taylorův vzorec | vyjadřuje pro polynom P(x) stupně n hodnotu polynomu P(x) pro x = x0 + h pomocí derivací
polynomu P(x) až do řádu n pro x = x0 (derivace polynomu P(x) počínaje (n + 1)-tým řádem
jsou všechny rovny nule): P(x0 + h) = P(x0) + (h/1!)P´(x0) + (h2/2!)P´´(x0) + ... + (hn/n!)P(n)(x0) Platnost T.v. se za určitých podmínek rozšiřuje i na funkce, které nejsou polynomy; tím se dostává tzv. Taylorova řada |
|||||||||||||||||||||||||
| tečna | t. křivky v jejím bodě A je limita posloupnosti přímek AB, kde B je bod křivky různý od A, jestliže se B blíží k A;
bod A se pak nazývá bodem dotyku tečny tečna ke křivce y = ƒ(x) má v bodě x = a rovnici y = ƒ'(a)x + [ƒ(a) - ƒ'(a)a] |
|||||||||||||||||||||||||
| tečná rovina | t.r. plochy v jejím bodě P je množina bodů všech tečen v bodě P ke všem křivkám ležícím na této ploše a procházejícím bodem P; je definována, pokud takovéto tečny existují | |||||||||||||||||||||||||
| tenzor | pojem vzniklý zobecněním vektoru (viz zde); udává se tzv. řád tenzoru; např. skalár je tenzor nultého řádu, vektor je tenzor prvního řádu. Riemannův tenzor: tenzor 4. řádu, popisující rozdíl geometrických vlastností daného prostoru od rovinného. V plochém prostoru je Riemannův tenzor všude roven nule. Ricciův tenzor: symetrický tenzor křivosti, který vzniká zúžením Riemannova tenzoru ve dvou indexech | |||||||||||||||||||||||||
| tenzor křivosti | G.F.B.Riemann; matematická rovnice s 256 složkami, která popisuje zakřivení časoprostoru později rovnici upravil (současně s D.Hilbertem) a získal sice rovnici se složitými matematickými objekty (tenzory), ale jinak je rovnice sama o sobě krásná a jednoduchá - deset nezávislých rovnic zabalených do rovnice jedné: Rμν - 1/2gμνR = 8πTμν levá strana rovnice říká jak je časoprostor na konkrétním místě zakřiven a pravá strana odkazuje na hustotu hmoty - energie, tlak, napětí, hustotu hybnosti a tok energie v tomto místě |
|||||||||||||||||||||||||
| tenzorový počet | "matematický jazyk" popisující geometrii na zakřivených površích a má tu vlastnost, že každá rovnice zachovávala svůj tvar při přechodu k jinému systému souřadnic | |||||||||||||||||||||||||
| teorie aritmetiky | (matematická) formální logika; zabývá se zkoumáním formálních aritmetických systémů a struktury v nich definovatelných množin přirozených čísel | |||||||||||||||||||||||||
| teorie čísel | zkoumá převážně vlastnosti přirozených čísel (např.: řešitelnost diofantovských rovnic, rozložení prvočísel) | |||||||||||||||||||||||||
| teorie důkazů | (matematická) formální logika; zabývá se vytvářením a zkoumáním různých formálních deduktivních systémů, které slouží jako základ pojmu formální důkaz | |||||||||||||||||||||||||
| teorie fluxionů | též fluxí; I.Newton; matematické odvětví známější pod názvem kalkul (viz zde) či matematická analýza | |||||||||||||||||||||||||
| teorie grafů | odvětví topologie; v současnosti se uplatňuje při analýze komunikačních sítí či navrhování počítačových obvodů | |||||||||||||||||||||||||
| teorie her | viz hra (zde) | |||||||||||||||||||||||||
| teorie množin | matematická teorie zabývající se studiem množin; pro matematiku má obrovský význam více viz teorie množin |
|||||||||||||||||||||||||
| teorie modelů | (matematická) formální logika; Alfred Tarski; zkoumá v matematické struktuře vztah mezi pravdivostí a tvrzením | |||||||||||||||||||||||||
| teorie pravděpodobnosti | obecná definice: zkoumá na jakých principech funguje náhoda; také viz zde 'pravděpodobnost' | |||||||||||||||||||||||||
| teorie uzlů | topologie; typický rys uzlu je způsob, jakým je uvázán, tzv. 'uzlovost' a právě tímto abstraktním pojmem se zabývá t.u. | |||||||||||||||||||||||||
| teorie vyčíslitelnosti | vědní obor na pomezí matematiky a informatiky, který zkoumá otázky algoritmické řešitelnosti problémů | |||||||||||||||||||||||||
| tětiva | t. křivky je libovolná úsečka, jejíž koncové body leží na křivce, zatímco ostatní její body na křivce neleží | |||||||||||||||||||||||||
| těžnice | t. trojúhelníku je úsečka spojující vrchol se středem protilehlé strany; trojúhelník má celkem tři t., které se všechny protínají v bodě zvaném těžiště | |||||||||||||||||||||||||
| Thalétova věta | tvrdí, že množina všech bodů, z nichž je úsečka AB vidět pod pravým úhlem, je kružnice s průměrem AB, s výjimkou bodů A, B více: Thaletovy věty |
|||||||||||||||||||||||||
| tchien-juan | Čína; metoda výpočtu druhé a třetí odmocniny, vyplývající z výpočtu druhé a třetí mocniny dvojčlenů, která je obsažena v traktátě "Matematika v devíti knihách" ze 2. stol. př.n.l.; slovo "tchien-juan" doslova znamená "nebeský prvek" a v čínské matematice se tak označovala "neznámá" | |||||||||||||||||||||||||
| topologický invariant | vlastnost sdílená všemi topologickými ekvivalentními povrchy (např. t.i. jimž se dají klasifikovat povrchy je počet hran, nebo dále orientovatelnost) | |||||||||||||||||||||||||
| topologie | teorie o vzájemné příbuznosti těles bez ohledu na jejich tvar; důležité je, kolik řezů můžeme v tělese provést, aniž by se rozdělilo na dvě části pův. vznikla jako zobecnění geometrie; nevšímá si metrických vlastností útvarů; také se nazývá podle Leibnize analysis situs; v topologii se dva útvary pokládají za ekvivalentní, jestliže si můžeme představit, že jsou sestrojeny jejich modely z dokonale elastického materiálu a že jeden z nich může být získán z druhého deformací bez "roztržení" a bez "zdvojení" - tento příklad umožňuje pojmenovat t. názvem "gumová geometrie" dále zde: topologie |
|||||||||||||||||||||||||
| torus | viz anuloid (zde) | |||||||||||||||||||||||||
| transfinitní aritmetika | viz (zde) 'nekonečno' | |||||||||||||||||||||||||
| transformace | speciální typ funkce (existuje jich velké množství, např. t. souřadnic, topologická t., lineární t. ... ad.) | |||||||||||||||||||||||||
| transpozice | jedná se o permutaci, která navzájem vyměňuje dva prvky a ostatní ponechává; každá t. má znaménko -1 | |||||||||||||||||||||||||
| tranzitivita | viz zde: relace (tranzitivní) | |||||||||||||||||||||||||
| trigonometrie | část geometrie, která užitím goniometrických funkcí (viz zde) řeší úlohy o trojúhelnících v rovině
(trigonometrie rovinná) nebo na kulové ploše (trigonometrie sférická); díky trigonometrickým metodám byly změřeny
první vzdálenosti hvězd goniometrické funkce - funkce původně vyjadřující vztah mezi velikostmi úhlů a stran v trojúhelníku; později byly jejich definice zobecněny pro argument, jímž může být velikost libovolného orientovaného úhlu vyjádřená ve stupních nebo v obloukové míře libovolným reálným číslem. Goniometrické funkce jsou sinus (značka sin), kosinus (cos), tangens (tg), kotangens (cotg), sekans (sec) a kosekans (cosec). Je-li α orientovaný úhel, jehož vrchol je umístěn do počátku kartézské soustavy souřadnic, počáteční rameno splývá s kladným směrem osy x a M = [x, y] je průsečík jednotkové kružnice s druhým ramenem úhlu α, je pro libovolné α definováno sin α = y, cos α = x; pro α ≠ (2k + 1)π/2, k celé, je tg α = sin α /cos α, sec α = 1/cos α; pro α ≠ π je cotg α = cos α /sin α, cosec α = 1/sin α sférická trigonometrie - obor matematiky, který zkoumá vztahy mezi prvky sférického trojúhelníku; ten je určen třemi body A, B a C na kulové ploše o poloměru R; jeho strany jsou oblouky hlavních kružnic |
|||||||||||||||||||||||||
| trisekce úhlu | úloha rozdělit daný úhel na tři stejné části; spolu s dalšími úlohami (kvadratura kruhu a Délský problém) tvoří tzv. "tři klasické starověké úlohy", které se nedají řešit pomocí kružítka a pravítka (euklidovská metoda); t.ú. lze řešit pomocí Nikomédovy konchoidy nebo pomocí Hippiovy kvadratrigy (viz KŘIVKY) | |||||||||||||||||||||||||
| trojhran | mnohohran o třech stěnách; v t. je součet velikostí hranových úhlů menší než 360o, velikost každého hranového úhlu je menší než součet ostatních dvou a větší než jejich rozdíl polární trojhran k danému trojhranu je t., jehož hrany jsou polopřímky vycházející z vrcholu daného t. kolmé k jeho stěnám a ležící vždy v poloprostoru obsahujícím hranu daného t., která neleží v příslušné rovině | |||||||||||||||||||||||||
| trojúhelník | mnohoúhelník, který má tři strany; navzájem kolmé strany pravoúhlého trojúhelníka se nazývají odvěsny a nejdelší strana se nazývá přepona;
je vždy konvexní; označíme-li délky stran t. symboly a, b, c, velikosti
úhlů protilehlých těmto stranám po řadě α, β, γ, obsah P a poloviční obvod s, pak platí:
|
|||||||||||||||||||||||||
| trojúhelníková čísla | pro Pythagorejce se jednalo o základní numerologická čísla; začneme v prvním řádku hodnotou jedna,
v dalším řádku hodnotu zvýšíme o 1, tedy 2, ve třetím řádku hodnota opět o jednu vyšší, tedy 3 etc (4, 5, 6 ...);
t.č. jsou součtem všech těchto hodnot, tedy 1, 3 (1+2), 6 (1+2+3), 10 (1+2+3+4) ... jedná se o počet bodů, které
je možno uspořádat do rovnostranného trojúhelníku (viz obrázek) K.F.Gauss odvodil obecný vzorec pro geometrickou strukturu t.č.: n(n + 1) / 2 |
|||||||||||||||||||||||||
| trs | viz přímka (zde) | |||||||||||||||||||||||||
| třída | obecně se jedná o souhrn prvků; obvykle se dnes třídou rozumí třída ekvivalence nebo rozkladu; v axiomatické teorii množin je třída obecnějším pojmem než množina třída křivky je maximální počet tečen, které lze ke křivce vést z bodu, jenž leží v její rovině | |||||||||||||||||||||||||
| třírozměrná geometrie | specializace G.Mongeho, který později přišel na způsob, který začali architekti a inženýři používat při projektování budov a konstrukcí strojů (půdorys, nárys, bokorys) | |||||||||||||||||||||||||
| Turingův stroj | Alan Turing, 30. léta 20. stol.; teorie abstraktního univerzálního počítače, byl schopen provádět běžné aritmetické operace | |||||||||||||||||||||||||
| tvořící přímka | libovolná přímka ležící na tzv. přímkové ploše, jejímž pohybem v prostoru vznikne tato plocha | |||||||||||||||||||||||||
| U | [ nahoru ] | |||||||||||||||||||||||||
| úhel | úhel dvou polopřímek je část roviny omezená dvěma polopřímkami r a s (zvané ramena úhlu) o témže počátku O (vrchol ú.);
mějme v rovině dvě poloroviny α a β, jejichž hraniční přímky mají společný bod O - pak jejich průnik se
nazývá konvexní úhel a jejich sjednocení je nekonvexní úhel dvě různoběžné přímky svírají čtyři úhly - vždy dva a dva jsou navzájem protilehlé (ramena jednoho jsou polopřímky opačné k ramenů druhého - tzv. vrcholové úhly); dva z těchto úhlů, které nejsou vrcholové, jsou tzv. vedlejší úhly a jejich součet je vždy 180o každý konvexní úhel, jehož velikost je menší než velikost pravého úhlu se nazývá ostrý úhel a analogicky, každý úhel, který je větší než pravý úhel je tupý úhel prostorový úhel - každá rotační kuželová plocha dělí prostor na dvě části, z nichž každá se nazývá p.ú. |
|||||||||||||||||||||||||
| úhlopříčka (mnohoúhelníku) | ú. m. je každá úsečka, jejímiž koncovými body jsou dva nesousední vrcholy mnohoúhelníku tělesová úhlopříčka mnohostěnu je každá úsečku, jejímiž koncovými body jsou vrcholy mnohostěnu nenáležíjící téže stěně | |||||||||||||||||||||||||
| úměra | rovnost dvou poměrů; zapisuje se a:b = c:d, kde a, d jsou vnější členy ú., b, c vnitřní členy ú. | |||||||||||||||||||||||||
| úměrnost | ú. na množině reálných čísel je funkce, která každému x přiřazuje reálné číslo ƒ(x) = kx, kde k ≠ 0, pak je to přímá úměra nebo každému nenulovému x přiřazuje reálné číslo ƒ(x) = k/x, kde k ≠ 0, a pak je to nepřímá úměra | |||||||||||||||||||||||||
| úsečka | ú. o koncových bodech A a B je množina bodů přímky AB, které leží mezi A a B | |||||||||||||||||||||||||
| uspořádaná dvojice | je tvořena dvěma prvky a, b, u nichž záleží na pořadí, v němž jsou uvažovány; značí se (a, b), na rozdíl od {a, b}, což označuje množinu | |||||||||||||||||||||||||
| uspořádání | viz relace (zde) | |||||||||||||||||||||||||
| uzlový bod | každý bod P křivky c, v němž má křivka c nejméně dvě různé tečny: bod v němž křivka protíná sebe samu | |||||||||||||||||||||||||
| V | [ nahoru ] | |||||||||||||||||||||||||
| válec | rotační válec; těleso vytvořené rotací obdélníku kolem jeho strany - tato strana je osa válce, strana s ní rovnoběžná je povrchová úsečka válce; válec je omezen dvěma kruhy zvanými podstavy a zakřivenou plochou (plášť), která je rozvinutelná do roviny | |||||||||||||||||||||||||
| variace | k-prvková variace (variace k-té třídy) z n prvků je uspořádaná k-tice navzájem různých prvků dané n-prvkové množiny; počet všech k-prvkových variací z n prvků je roven n!/(n-k)!, kde vykřičník je faktoriál | |||||||||||||||||||||||||
| varieta | B.Riemann; zobecnění povrchu pro vyšší rozměry | |||||||||||||||||||||||||
| vektor | aritmetický vektor je uspořádaná n-tice a, a2, …, an
čísel (např. reálných). Jsou-li zapsány v řádku, mluví se o
řádkovém vektoru, jsou-li ve sloupci, vznikne vektor sloupcový. Geometrický
vektor je množina všech navzájem rovnoběžných, stejně dlouhých a stejně
orientovaných úseček. V tomto smyslu se vektor geometrický někdy nazývá též
volný vektor. Vybere-li se jedna úsečka z této množiny, hovoří se o vázaném
vektoru umístěném v bodě, který je počátečním bodem uvažované orientované
úsečky; vektorový prostor, neprázdná množina V, ve které pro každou
dvojici u, v X V a pro každé reálné (popř. komplexní) číslo c je jednoznačně
definován součet u + v ∈ V a součin cu ∈ V. Operace sčítání je asociativní a
komutativní a existuje takový prvek o ∈ V, že u + o = u – o = u. Operace
násobení splňuje vztahy: 1u = u, c(du) = (cd)u, (c + d)u = cu + du, c(u + v)
= cu + cv pro včechna u, v ∈ V a všechna čísla c, d. Prvky vektorového
prostoru se nazývají vektory vektor rychlosti - rychlost a směr rychlosti pohybu tělesa |
|||||||||||||||||||||||||
| vektorové pole | matematická struktura (rovnice), popisující silové pole (např. magnetické), která určuje velikost i směr síly v každém bodě (i čase) | |||||||||||||||||||||||||
| Velká Fermatova věta | neexistují celá čísla a,b,c pro která platí an + bn =
cn kde n je celé číslo větší než 2 franc. matematik Pierre Fermat si r. 1637 napsal do učebnice toto tvrzení a připojil poznámku, že nalezl i důkaz tohoto tvrzení, avšak ten již nepublikoval; důkaz jeho tvrzení byl nalezen až r. 1994 (Andrew Wiles) a tento "objev" se stal matematickou událostí 20. století |
|||||||||||||||||||||||||
| Vennův diagram | grafické znázornění množiny | |||||||||||||||||||||||||
| vepsaný | termín vztahující se ke dvěma geometrickým útvarům a, b; je-li útvar a vepsán útvaru b, pak říkáme, že útvar b je opsán útvaru a | |||||||||||||||||||||||||
| věstonická vrubovka | 18 cm dlouhá lýtková kost mladého vlka s 55 zářezy, nalezená 19. 8. 1936 u Dolních Věstonic (K.Absolon); připomínala počítací hůlky (rabuše, rováše), o nichž je známo, že patřily (ovšem mnohem později) mezi početní instrumenty negramotných lidí leckde na světě, například v Evropě až do 20. stol., a v některých oblastech světa se používají dodnes | |||||||||||||||||||||||||
| věta | tvrzení dokazaztelné na základě axiomů, definic nebo jiných vět již dokázaných; z předpokladu (jehož pravdivost se předpokládá) se řetězcem implikací dochází k závěru, který je tvrzením věty; tento postup se pak nazývá důkaz věty obrácená věta; věta je obrácená k jiné větě, jestliže z ní vznikne vzájemnou výměnou předpokladu a tvrzení | |||||||||||||||||||||||||
| věta duální | viz zde 'princip duality' | |||||||||||||||||||||||||
| věta o neúplnosti | K.Gödel (1931); matematická logika; tvrzení, že pokud vytvoříme pro dostatečně bohatou matematrickou teorii bezesporný systém axiomů, pak je tento systém nutně neúplný - vždy se najdou nějaké otázky, na které nebudeme na základě těchto axiomů moci odpovědět | |||||||||||||||||||||||||
| vrstva | průnik dvou poloprostorů, jejichž hraniční roviny jsou rovnoběžné a každý z uvedených poloprostorů obsahuje hraniční rovinu druhého | |||||||||||||||||||||||||
| výraz | vyjadřuje souhrn operací s prvky dané množiny, které se mají provést podle předem daných pravidel neurčitý výraz - výraz u něhož nelze použít základních vět o limitě součtu, součinu, podílu, mocniny či logaritmu | |||||||||||||||||||||||||
| výrokové proměnné | jedná se o termín z matematického oboru formální logiky; stejně jako v algebře pracujeme s neznámými proměnnými a, b, c, tak
protože nás jednotlivé výroky (nyní) nezajímají, označíme si jednotlivé výroky jako A, B, C; a stejně jako v algebře užíváme
pro početní úkony různé symboly (+ - x /), tak i logická struktura výrokových spojení má své symboly:
|
|||||||||||||||||||||||||
| výška | výška trojúhelníku - kolmice vedená vrcholem k protilehlé straně (přímka) nebo úsečka na této kolmici mezi vrcholem a protilehlou stranou, nebo délka této úsečky (číslo) výška rovnoběžníku - vzdálenost protilehlých stran a výška lichoběžníku je vzdálenost rovnoběžných stran výška jehlanu (kužele) je vzdálenost vrcholu od roviny podstavy výška hranolu (válce, komolého kuželu a komolého jehlanu) - vzdálenost rovin obou podstav | |||||||||||||||||||||||||
| vývojový diagram | schematické vyjádření algoritmu | |||||||||||||||||||||||||
| vzdálenost | (geometrie) vzdálenost dvou bodů A, B je délka úsečky AB; vzdálenost bodu A od přímky p (od roviny r) je vzdálenost bodu A od paty kolmice sestrojené z bodu A k přímce p (rovině r) | |||||||||||||||||||||||||
| vzorec | obecně se jedná o rovnost, která vyjadřuje hodnotu jedné proměnné pomocí jiných | |||||||||||||||||||||||||
| Z | [ nahoru ] | |||||||||||||||||||||||||
| zábavná matematika | letmá odbočka od vážné matematiky k té příjemější, snad i zábavné... viz zde |
|||||||||||||||||||||||||
| základní věta algebry | v množině komplexních čísel má řešení každá polynomiální rovnice (algebraická rovnice n-tého stupně) ve tvaru: anxn + an-1xn-1 + ... a1x + a0 = 0, kde a0, ..., an jsou komplexní čísla |
|||||||||||||||||||||||||
| základní věta aritmetiky | Eukleides; každé přirozené číslo je buď samo prvočíslem, nebo má jednoznačně určený prvočíselný rozklad (až na pořadí) | |||||||||||||||||||||||||
| závorky | grafický znak, kterého se užívá ve výrazech; z. značí, že je nejprve třeba určit hodnotu výrazu v nich obsaženého a potom ji dosadit do zbývající části výrazu; užívá se tří typů, zde uvedeny v obvyklém pořadí: () - [] - {} | |||||||||||||||||||||||||
| Zenonova posloupnost | viz zde 'Achilles a želva'; posloupnost má nekonečně mnoho členů vycházející právě z paradoxu Achilles a želva; pokud tyto členy sečteme, ač jich je nekonečně mnoho, dostáváme číslo konečné: 1/2 + 1/4 + 1/8 + ... + 1/64 + ... = 2 | |||||||||||||||||||||||||
| zero | anglický (a v mnoha jiných jazycích) termín pro 'nulu'; termín má indické a arabské kořeny - současné slovo je výsledkem různých přeměn hindského slova 'šunja' (nula, prázdno), které se transformovalo přes arabštinu a latinu: arabové přeměnili slovo šunja na 'sifr' a pak se v latině slovo přeměnilo na 'zefirus', což je základem slova zero, ale také "vytvořilo" všeobecný pojem ve francouzštině 'chiffre', češtině 'cifra', ale také šifra ... | |||||||||||||||||||||||||
| zlatý řez | z.ř. úsečky AB je úsečka AC obsažená v AB, jejíž délka je geometrickým průměrem délek úseček AB a BC; má-li
úsečka AB délku a, pak její zlatý řez má délku a(√5 - 1)/2 rozdělme úsečku na dva díly tak, aby poměr menší části k větší byl roven poměru větší části k celé délce úsečky; pro jednoduchost předpokládejme, že malý díl úsečky je dlouhý 1 metr a velký je tedy dlouhý 'x' metrů - pak délka celé úsečky je 1 + x; převedením vztahu do algebraické podoby zjistíme, že poměr malého dílu k většímu je 1/x, zatímco poměr velkého dílu a celé úsečky je x / (1 + x) protože poměr malého dílu k velkému dílu je roven poměru velkého dílu k celé úsečce, můžeme položit rovnítko a dostaneme vztah x / (1 + x) = 1 / x násobíme pro zkrácení rovnice výrazem 'x' a dostaneme x2 / (1 + x) = 1 po vynásobení obou stran´rovnice výrazem (1 + x), dostaneme x2 = 1 + x, z čehož dostáváme běžnou kvadratickou rovnici x2 - x - 1 = 0 řešením této rovnice je jeden kladný kořen: (1 + √5)/2 = 1,618 ... více viz: zlatý řez |
|||||||||||||||||||||||||
| zlomek | definujme zlomek jako uspořádanou dvojici (a,b) čísel a ∈ N, b ∈ N | |||||||||||||||||||||||||
| zobrazení | z. množiny A do množiny B přiřazuje každému prvku a ∈ A právě jeden prvek množiny B inverzní zobrazení - je-li vzájemně jednoznačné zobrazení množiny A na množinu B, pak každému b ∈ B přiřaďme ten prvek a ∈ A, kterému zobrazení z přiřazuje prvek b složené zobrazení - budiž z zobrazení množiny A do množiny B a u zobrazení množiny B do množiny C; složeným zobrazením u • z rozumíme zobrazení množiny A do množiny C, které každému prvku a ∈ A přiřazuje ten prvek množiny C, který zobrazení u přiřazuje obrazu prvku a v zobrazení z |